本来笔者已经决心不玩RNN了，但是在上个星期思考时忽然意识到RNN实际上对应了ODE（常微分方程）的数值解法，这为我一直以来想做的事情——用深度学习来解决一些纯数学问题——提供了思路。事实上这是一个颇为有趣和有用的结果，遂介绍一翻。顺便地，本文也涉及到了自己动手编写RNN的内容，所以本文也可以作为编写自定义的RNN层的一个简单教程。

注：本文并非前段时间的热点“神经ODE”的介绍（但有一定的联系）。

RNN基本 #

什么是RNN？ #

众所周知，RNN是“循环神经网络（Recurrent Neural Network）”，跟CNN不同，RNN可以说是一类模型的总称，而并非单个模型。简单来讲，只要是输入向量序列$(\boldsymbol{x}_1,\boldsymbol{x}_2,\dots,\boldsymbol{x}_T)$，输出另外一个向量序列$(\boldsymbol{y}_1,\boldsymbol{y}_2,\dots,\boldsymbol{y}_T)$，并且满足如下递归关系
$$\boldsymbol{y}_t=f(\boldsymbol{y}_{t-1}, \boldsymbol{x}_t, t)\tag{1}$$
的模型，都可以称为RNN。也正因为如此，原始的朴素RNN，还有改进的如GRU、LSTM、SRU等模型，我们都称为RNN，因为它们都可以作为上式的一个特例。还有一些看上去与RNN没关的内容，比如前不久介绍的CRF的分母的计算，实际上也是一个简单的RNN。

说白了，RNN其实就是递归计算。

自己编写RNN #

这里我们先介绍如何用Keras简单快捷地编写自定义的RNN。

事实上，不管在Keras还是纯tensorflow中，要自定义自己的RNN都不算复杂。在Keras中，只要写出每一步的递归函数；而在tensorflow中，则稍微复杂一点，需要将每一步的递归函数封装为一个RNNCell类。下面介绍用Keras实现最基本的一个RNN：
$$\boldsymbol{y}_t=\tanh(\boldsymbol{W}_1 \boldsymbol{y}_{t-1} + \boldsymbol{W}_2 \boldsymbol{x}_t + \boldsymbol{b})\tag{2}$$
代码非常简单：

#! -*- coding: utf-8- -*-

from keras.layers import Layer
import keras.backend as K


class My_RNN(Layer):

    def __init__(self, output_dim, **kwargs):
        self.output_dim = output_dim # 输出维度
        super(My_RNN, self).__init__(**kwargs)

    def build(self, input_shape): # 定义可训练参数
        self.kernel1 = self.add_weight(name='kernel1',
                                      shape=(self.output_dim, self.output_dim),
                                      initializer='glorot_normal',
                                      trainable=True)
        self.kernel2 = self.add_weight(name='kernel2',
                                      shape=(input_shape[-1], self.output_dim),
                                      initializer='glorot_normal',
                                      trainable=True)
        self.bias = self.add_weight(name='bias',
                                      shape=(self.output_dim,),
                                      initializer='glorot_normal',
                                      trainable=True)

    def step_do(self, step_in, states): # 定义每一步的迭代
        step_out = K.tanh(K.dot(states[0], self.kernel1) +
                          K.dot(step_in, self.kernel2) +
                          self.bias)
        return step_out, [step_out]

    def call(self, inputs): # 定义正式执行的函数
        init_states = [K.zeros((K.shape(inputs)[0],
                                self.output_dim)
                              )] # 定义初始态(全零)
        outputs = K.rnn(self.step_do, inputs, init_states) # 循环执行step_do函数
        return outputs[0] # outputs是一个tuple，outputs[0]为最后时刻的输出，
                          # outputs[1]为整个输出的时间序列，output[2]是一个list，
                          # 是中间的隐藏状态。

    def compute_output_shape(self, input_shape):
        return (input_shape[0], self.output_dim)

可以看到，虽然代码行数不少，但大部分都只是固定格式的语句，真正定义rnn的，是step_do这个函数，这个函数接受两个输入：step_in和states。其中step_in是一个(batch_size, input_dim)的张量，代表当前时刻的样本$\boldsymbol{x}_t$，而states是一个list，代表$\boldsymbol{y}_{t-1}$及一些中间变量；特别要注意的是，states是一个张量的list，而不是单个张量，这是因为在递归过程中可能要同时传递多个中间变量，而不仅仅是$\boldsymbol{y}_{t-1}$一个，比如LSTM就需要有两个态张量。最后step_do要返回$\boldsymbol{y}_t$和新的states，这是step_do这步的函数的编写规范。

而K.rnn这个函数，接受三个基本参数（还有其他参数，请自行看官方文档），其中第一个参数就是刚才写好的step_do函数，第二个参数则是输入的时间序列，第三个是初始态，跟前面说的states一致，所以很自然init_states也是一个张量的list，默认情况下我们会选择全零初始化。

ODE基本 #

什么是ODE？ #

ODE就是“常微分方程（Ordinary Differential Equation）”，这里指的是一般的常微分方程组：
$$\dot{\boldsymbol{x}}(t)=\boldsymbol{f}\big(\boldsymbol{x}(t), t\big)\tag{3}$$
研究ODE的领域通常也直接称为“动力学”、“动力系统”，这是因为牛顿力学通常也就只是一组ODE而已。

ODE可以产生非常丰富的函数。比如$e^t$其实就是$\dot{x}=x$的解，$\sin t$和$\cos t$都是$\ddot{x}+x=0$的解（初始条件不同）。事实上，我记得确实有一些教程是直接通过微分方程$\dot{x}=x$来定义$e^t$函数的。除了这些初等函数，很多我们能叫得上名字但不知道是什么鬼的特殊函数，都是通过ODE导出来的，比如超几何函数、勒让德函数、贝塞尔函数...

总之，ODE能产生并且已经产生了各种各样千奇百怪的函数～

数值解ODE #

能精确求出解析解的ODE其实是非常少的，所以很多时候我们都需要数值解法。

ODE的数值解已经是一门非常成熟的学科了，这里我们也不多做介绍，仅引入最基本的由数学家欧拉提出来的迭代公式：
$$\boldsymbol{x}(t + h) = \boldsymbol{x}(t) + h \boldsymbol{f}\big(\boldsymbol{x}(t), t\big)\tag{4}$$
这里的$h$是步长。欧拉的解法来源很简单，就是用
$$\frac{\boldsymbol{x}(t + h) - \boldsymbol{x}(t)}{h}\tag{5}$$
来近似导数项$\dot{\boldsymbol{x}}(t)$。只要给定初始条件$\boldsymbol{x}(0)$，我们就可以根据$(4)$一步步迭代算出每个时间点的结果。

ODE与RNN #

ODE也是RNN #

大家仔细对比$(4)$和$(1)$，发现有什么联系了吗？

在$(1)$中，$t$是一个整数变量，在$(4)$中，$t$是一个浮点变量，除此之外，$(4)$跟$(1)$貌似就没有什么明显的区别了。事实上，在$(4)$中我们可以以$h$为时间单位，记$t=nh$，那么$(4)$变成了
$$\boldsymbol{x}\big((n+1)h\big) = \boldsymbol{x}(nh) + h \boldsymbol{f}\big(\boldsymbol{x}(nh), nh\big)\tag{6}$$
可以看到现在$(6)$中的时间变量$n$也是整数了。

这样一来，我们就知道：ODE的欧拉解法$(4)$实际上就是RNN的一个特例罢了。这里我们也许可以间接明白为什么RNN的拟合能力如此之强了（尤其是对于时间序列数据），我们看到ODE可以产生很多复杂的函数，而ODE只不过是RNN的一个特例罢了，所以RNN也就可以产生更为复杂的函数了。

用RNN解ODE #

于是，我们就可以写一个RNN来解ODE了，比如《两生物种群竞争模型》中的例子：
$$\left\{\begin{aligned}\frac{dx_1}{dt}=r_1 x_1\left(1-\frac{x_1}{N_1}\right)-a_1 x_1 x_2 \\
\frac{dx_2}{dt}=r_2 x_2\left(1-\frac{x_2}{N_2}\right)-a_2 x_1 x_2\end{aligned}\right.\tag{7}$$
我们可以写出

#! -*- coding: utf-8- -*-

from keras.layers import Layer
import keras.backend as K


class ODE_RNN(Layer):

    def __init__(self, steps, h, **kwargs):
        self.steps = steps
        self.h = h
        super(ODE_RNN, self).__init__(**kwargs)

    def step_do(self, step_in, states): # 定义每一步的迭代
        x = states[0]
        r1,r2,a1,a2,iN1,iN2 = 0.1,0.3,0.0001,0.0002,0.002,0.003
        _1 = r1 * x[:,0] * (1 - iN1 * x[:,0]) - a1 * x[:,0] * x[:,1]
        _2 = r2 * x[:,1] * (1 - iN2 * x[:,1]) - a2 * x[:,0] * x[:,1]
        _1 = K.expand_dims(_1, 1)
        _2 = K.expand_dims(_2, 1)
        _ = K.concatenate([_1, _2], 1)
        step_out = x + self.h * _
        return step_out, [step_out]

    def call(self, inputs): # 这里的inputs就是初始条件
        init_states = [inputs]
        zeros = K.zeros((K.shape(inputs)[0],
                         self.steps,
                         K.shape(inputs)[1])) # 迭代过程用不着外部输入，所以
                                              # 指定一个全零输入，只为形式上的传入
        outputs = K.rnn(self.step_do, zeros, init_states) # 循环执行step_do函数
        return outputs[1] # 这次我们输出整个结果序列

    def compute_output_shape(self, input_shape):
        return (input_shape[0], self.steps, input_shape[1])


from keras.models import Sequential
import numpy as np
import matplotlib.pyplot as plt


steps,h = 1000,0.1

M = Sequential()
M.add(ODE_RNN(steps, h, input_shape=(2,)))
M.summary()

# 直接前向传播就输出解了
result = M.predict(np.array([[100, 150]]))[0] # 以[100, 150]为初始条件进行演算
times = np.arange(1, steps+1) * h

# 绘图
plt.plot(times, result[:,0])
plt.plot(times, result[:,1])
plt.savefig('test.png')

整个过程很容易理解，只不过有两点需要指出一下。首先，由于方程组$(7)$只有两维，而且不容易写成矩阵运算，因此我在step_do函数中是直接逐位操作的（代码中的x[:,0],x[:,1]），如果方程本身维度较高，而且能写成矩阵运算，那么直接利用矩阵运算写会更加高效；然后，我们可以看到，写完整个模型之后，直接predict就输出结果了，不需要“训练”。

RNN解两物种的竞争模型

RNN解两物种的竞争模型

反推ODE参数 #

前一节的介绍也就是说，RNN的前向传播跟ODE的欧拉解法是对应的，那么反向传播又对应什么呢？

在实际问题中，有一类问题称为“模型推断”，它是在已知实验数据的基础上，猜测这批数据符合的模型（机理推断）。这类问题的做法大概分两步，第一步是猜测模型的形式，第二步是确定模型的参数。假定这批数据可以由一个ODE描述，并且这个ODE的形式已经知道了，那么就需要估计里边的参数。

如果能够用公式完全解出这个ODE，那么这就只是一个非常简单的回归问题罢了。但前面已经说过，多数ODE都没有公式解，所以数值方法就必须了。这其实就是ODE对应的RNN的反向传播所要做的事情：前向传播就是解ODE（RNN的预测过程），反向传播自然就是推断ODE的参数了（RNN的训练过程）。这是一个非常有趣的事实：ODE的参数推断是一个被研究得很充分的课题，然而在深度学习这里，只是RNN的一个最基本的应用罢了。

我们把刚才的例子的微分方程的解数据保存下来，然后只取几个点，看看能不能反推原来的微分方程出来，解数据为：
$$\begin{array}{c|ccccccc}
\hline
\text{时间} & 0 & 10 & 15 & 30 & 36 & 40 & 42\\
\hline
x_1 & 100 & 165 & 197 & 280 & 305 & 318 & 324\\
\hline
x_2 & 150 & 283 & 290 & 276 & 269 & 266 & 264\\
\hline
\end{array}$$
假设就已知这有限的点数据，然后假定方程$(7)$的形式，求方程的各个参数。我们修改一下前面的代码：

#! -*- coding: utf-8- -*-

from keras.layers import Layer
import keras.backend as K


def my_init(shape, dtype=None): # 需要定义好初始化，这相当于需要实验估计参数的量级
    return K.variable([0.1, 0.1, 0.001, 0.001, 0.001, 0.001])


class ODE_RNN(Layer):
    
    def __init__(self, steps, h, **kwargs):
        self.steps = steps
        self.h = h
        super(ODE_RNN, self).__init__(**kwargs)
    
    def build(self, input_shape): # 将原来的参数设为可训练的参数
        self.kernel = self.add_weight(name='kernel', 
                                      shape=(6,),
                                      initializer=my_init,
                                      trainable=True)
    def step_do(self, step_in, states): # 定义每一步的迭代
        x = states[0]
        r1,r2,a1,a2,iN1,iN2 = (self.kernel[0], self.kernel[1],
                               self.kernel[2], self.kernel[3],
                               self.kernel[4], self.kernel[5])
        _1 = r1 * x[:,0] * (1 - iN1 * x[:,0]) - a1 * x[:,0] * x[:,1]
        _2 = r2 * x[:,1] * (1 - iN2 * x[:,1]) - a2 * x[:,0] * x[:,1]
        _1 = K.expand_dims(_1, 1)
        _2 = K.expand_dims(_2, 1)
        _ = K.concatenate([_1, _2], 1)
        step_out = x + self.h * K.clip(_, -1e5, 1e5) # 防止梯度爆炸
        return step_out, [step_out]
    
    def call(self, inputs): # 这里的inputs就是初始条件
        init_states = [inputs]
        zeros = K.zeros((K.shape(inputs)[0],
                         self.steps,
                         K.shape(inputs)[1])) # 迭代过程用不着外部输入，所以
                                              # 指定一个全零输入，只为形式上的传入
        outputs = K.rnn(self.step_do, zeros, init_states) # 循环执行step_do函数
        return outputs[1] # 这次我们输出整个结果序列
    
    def compute_output_shape(self, input_shape):
        return (input_shape[0], self.steps, input_shape[1])



from keras.models import Sequential
from keras.optimizers import Adam
import numpy as np
import matplotlib.pyplot as plt


steps,h = 50, 1 # 用大步长，减少步数，削弱长时依赖，也加快推断速度
series = {0: [100, 150],
          10: [165, 283],
          15: [197, 290],
          30: [280, 276],
          36: [305, 269],
          40: [318, 266],
          42: [324, 264]}

M = Sequential()
M.add(ODE_RNN(steps, h, input_shape=(2,)))
M.summary()

# 构建训练样本
# 其实就只有一个样本序列，X为初始条件，Y为后续时间序列
X = np.array([series[0]])
Y = np.zeros((1, steps, 2))

for i,j in series.items():
    if i != 0:
        Y[0, int(i/h)-1] += series[i]

# 自定义loss
# 在训练的时候，只考虑有数据的几个时刻，没有数据的时刻被忽略
def ode_loss(y_true, y_pred):
    T = K.sum(K.abs(y_true), 2, keepdims=True)
    T = K.cast(K.greater(T, 1e-3), 'float32')
    return K.sum(T * K.square(y_true - y_pred), [1, 2])

M.compile(loss=ode_loss,
          optimizer=Adam(1e-4))

M.fit(X, Y, epochs=10000) # 用低学习率训练足够多轮

# 用训练出来的模型重新预测，绘图，比较结果
result = M.predict(np.array([[100, 150]]))[0]
times = np.arange(1, steps+1) * h

plt.clf()
plt.plot(times, result[:,0], color='blue')
plt.plot(times, result[:,1], color='green')
plt.plot(series.keys(), [i[0] for i in series.values()], 'o', color='blue')
plt.plot(series.keys(), [i[1] for i in series.values()], 'o', color='green')
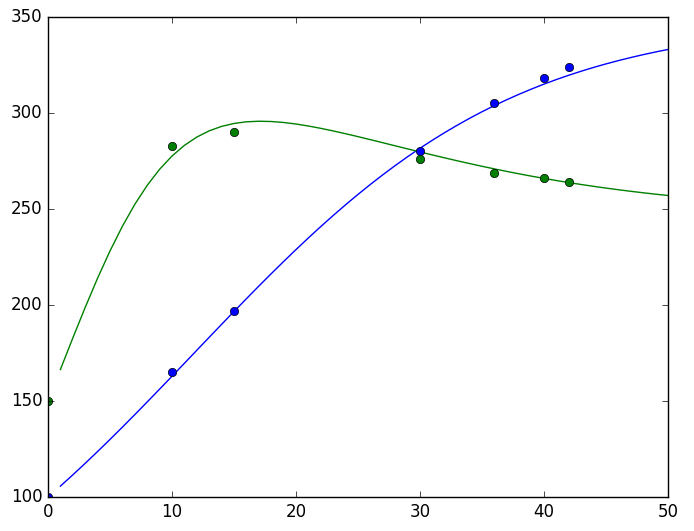
plt.savefig('test.png')

结果可以用一张图来看：

RNN做ODE的参数估计效果（散点：有限的实验数据，曲线：估计出来的模型）

RNN做ODE的参数估计效果（散点：有限的实验数据，曲线：估计出来的模型）


显然结果是让人满意的。

又到总结 #

本文在一个一般的框架下介绍了RNN模型及其在Keras下的自定义写法，然后揭示了ODE与RNN的联系。在此基础上，介绍了用RNN直接求解ODE以及用RNN反推ODE参数的基本思路。需要提醒读者的是，在RNN模型的反向传播中，要谨慎地做好初始化和截断处理处理，并且选择好学习率等，以防止梯度爆炸的出现（梯度消失只是优化得不够好，梯度爆炸则是直接崩溃了，解决梯度爆炸问题尤为重要）。

总之，梯度消失和梯度爆炸在RNN中是一个很经典的困难，事实上，LSTM、GRU等模型的引入，根本原因就是为了解决RNN的梯度消失问题，而梯度爆炸则是通过使用tanh或sigmoid激活函数来解决的。但是如果用RNN解决ODE的话，我们就没有选择激活函数的权利了（激活函数就是ODE的一部分），所以只能谨慎地做好初始化及其他处理。据说，只要谨慎做好初始化，普通RNN中用relu作为激活函数都是无妨的～

转载到请包括本文地址：https://kexue.fm/archives/5643

更详细的转载事宜请参考：《科学空间FAQ》

如果您还有什么疑惑或建议，欢迎在下方评论区继续讨论。

如果您觉得本文还不错，欢迎分享/打赏本文。打赏并非要从中获得收益，而是希望知道科学空间获得了多少读者的真心关注。当然，如果你无视它，也不会影响你的阅读。再次表示欢迎和感谢！

如果您需要引用本文，请参考：

苏剑林. (Jun. 23, 2018). 《貌离神合的RNN与ODE：花式RNN简介 》[Blog post]. Retrieved from https://kexue.fm/archives/5643

@online{kexuefm-5643,
        title={貌离神合的RNN与ODE：花式RNN简介},
        author={苏剑林},
        year={2018},
        month={Jun},
        url={\url{https://kexue.fm/archives/5643}},
}