n个正态随机数的最大值的渐近估计

设$z_1,z_2,\cdots,z_n$是$n$个从标准正态分布中独立重复采样出来的随机数，由此我们可以构造出很多衍生随机变量，比如$z_1+z_2+\cdots+z_n$，它依旧服从正态分布，又比如$z_1^2+z_2^2+\cdots+z_n^2$，它服从卡方分布。这篇文章我们来关心它的最大值$z_{\max} = \max\{z_1,z_2,\cdots,z_n\}$的分布信息，尤其是它的数学期望$\mathbb{E}[z_{\max}]$。

先看结论 #

关于$\mathbb{E}[z_{\max}]$的基本估计结果是：

设$z_1,z_2,\cdots,z_n\sim\mathcal{N}(0,1)$，$z_{\max} = \max\{z_1,z_2,\cdots,z_n\}$，那么 \begin{equation}\mathbb{E}[z_{\max}]\sim \sqrt{2\log n}\label{eq:E-z-max}\end{equation}

这里式$\eqref{eq:E-z-max}$的$\sim$的含义是：
\begin{equation}\lim_{n\to\infty} \frac{\mathbb{E}[z_{\max}]}{\sqrt{2\log n}} = 1\end{equation}
由此可见随着$n$的增长，这个结果相对来说是越来越准的。更准一点的结果则是
\begin{equation}\mathbb{E}[z_{\max}]\sim \sqrt{2\log \frac{n}{\sqrt{2\pi}}}\end{equation}
我们可以用Numpy验证它们：

import numpy as np

n = 4096
z = np.random.randn(10000, n)
E_z_max = z.max(axis=1).mean()  # ≈ 3.63
approx1 = np.sqrt(2 * np.log(n))  # ≈ 4.08
approx2 = np.sqrt(2 * np.log(n / np.sqrt(2 * np.pi)))  # ≈ 3.85

快速上界 #

对于上述结论，本文将给出三个证明。第一个证明来自帖子《Expectation of the maximum of gaussian random variables》内 @Sivaraman 的回答，它其实只能证明$\mathbb{E}[z_{\max}] \leq \sqrt{2\log n}$，但证明过程也颇为精彩，值得学习一番。

证明巧妙地利用了$\exp$的凸性：对于任意$t > 0$，可以写出
\begin{equation}\exp(t\mathbb{E}[z_{\max}]) \leq \mathbb{E}[\exp(t z_{\max})] = \mathbb{E}[\max_i \exp(t z_i)]\leq \sum_{i=1}^n\mathbb{E}[\exp(t z_i)] = n \exp(t^2 / 2)\end{equation}
第一个$\leq$是基于Jensen不等式，第二个$\leq$则是将最大值换成求和。现在两边取对数，整理得到
\begin{equation}\mathbb{E}[z_{\max}] \leq \frac{\log n}{t} + \frac{t}{2}\end{equation}
注意这是对任意$t > 0$都是成立的，所以我们可以选取让右端最小的$t$，使得近似程度最高。由基本不等式可知右端最小值在$t=\sqrt{2\log n}$取到，代入上式即得
\begin{equation}\mathbb{E}[z_{\max}] \leq \sqrt{2\log n}\end{equation}
该推导的特点是简单快捷，不需要多少额外的前置知识，但它理论上只是一个上界，只不过它出乎意料地准确，刚好也是渐近结果。

常规思路 #

对于习惯按部就班地推公式的人（比如笔者）来说，上述推导多少有种“邪修”的感觉了，因为常规解法应该是先求出$z_{\max}$的概率密度函数，然后再通过积分来计算期望，这一节我们就按照这个思路来推导。

概率密度 #

对于1维分布来说，概率密度函数和累积分布函数是可以互推的“一体两面”，而求$z_{\max}$的概率密度正需要累积分布函数来辅助推导。标准正态分布的概率密度是$p(z)=\exp(-z^2/2)/\sqrt{2\pi}$，累积分布函数$\Phi(z)=\int_{-\infty}^z p(x)dx$是一个非初等函数，它的含义是随机变量小于等于$z$的概率。

要求$z_{\max}$的累积分布函数，即求$P(z_{\max} \leq z)$，易知$z_{\max} \leq z$等价于$z_1 \leq z, z_2\leq z, \cdots, z_n\leq z$同时成立，而$z_i$是独立采样的，所以它们同时成立的概率，等于各自成立的概率之积
\begin{equation}P(z_{\max} \leq z) = \prod_{i=1}^n P(z_i \leq z) = [\Phi(z)]^n \end{equation}
所以$z_{\max}$的累积分布函数就是$[\Phi(z)]^n$，一个非常简洁的结果。注意我们还没用到$z$服从正态分布这一条件，所以这事实上是一个通用结果，即从任意分布独立重复采样的$n$个数，它的最大值的累积分布函数，是原始分布的累积分布函数的$n$次方。现在对它求导，就得到$z_{\max}$的概率密度函数$p_{\max}(z)$：
\begin{equation}p_{\max}(z) = n[\Phi(z)]^{n-1} p(z) \end{equation}

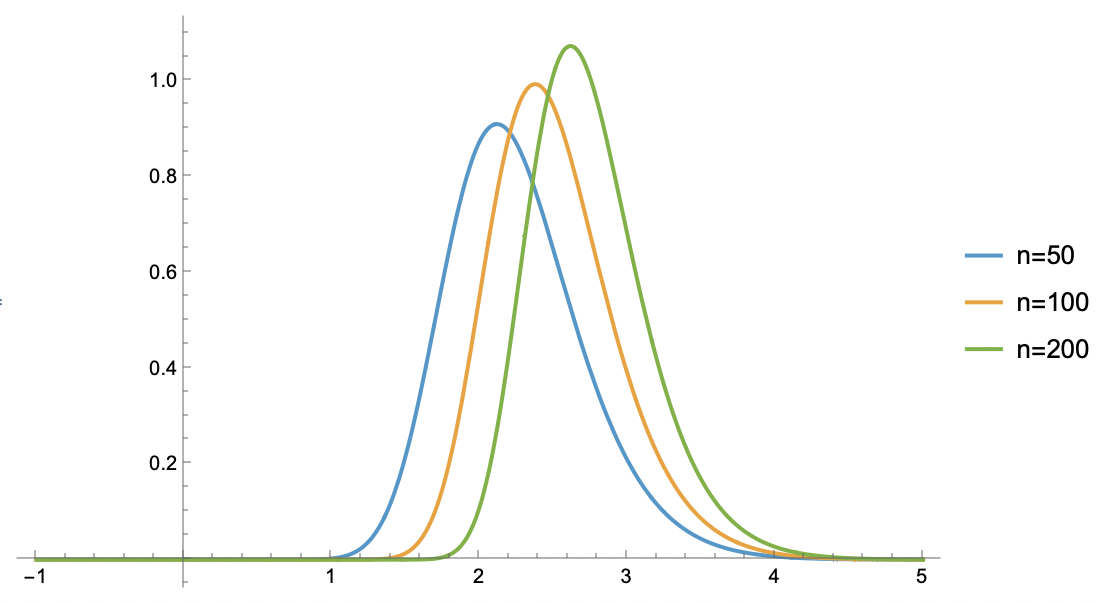
$n=50,100,200$时$p_{\max}(z)$的图像如下：

几个不同的n对应的p_max(z) 图像

拉普拉斯 #

有了概率密度函数后，理论上我们就可以积分算期望：
\begin{equation}\mathbb{E}[z_{\max}] = \int_{-\infty}^{\infty} z\, p_{\max}(z) dz\end{equation}
但很明显，这个积分并不好算，所以我们要寻找某个好算的近似。从上面的图像可以看出，$p_{\max}(z)$的形状其实也类似于正态分布的倒钟形，所以很自然想到寻找正态分布近似，这也叫做“拉普拉斯近似（Laplace Approximation）”。

寻找正态分布近似的第一步，是要找到倒钟形曲线的最大值点，然后在该点处将$\log p_{\max}(z)$展开到二阶，如果只是为了求均值，那么找到最大值点就行了，因为正态分布的均值就是概率密度的最大值点。为了找到这个最大值点$z_*$，我们先求$\log p_{\max}(z)$：
\begin{equation}\begin{aligned}
\log p_{\max}(z) =&\, \log n + (n-1)\log \Phi(z) + \log p(z) \\
=&\, \log n + (n-1)\log \Phi(z) - \frac{z^2}{2} - \frac{1}{2}\log 2\pi
\end{aligned}\end{equation}
对$z$求导得
\begin{equation}\frac{d}{dz}\log p_{\max}(z) = (n-1) \frac{p(z)}{\Phi(z)} - z = \frac{(n-1)\exp(-z^2/2)}{\Phi(z) \sqrt{2\pi}} - z\end{equation}
让它等于0，可以整理得
\begin{equation}z_* = \sqrt{2\log\frac{n-1}{z_*\Phi(z_*)\sqrt{2\pi}}}\label{eq:z}\end{equation}

近似求解 #

接下来的任务就是解方程$\eqref{eq:z}$，当然我们也不需要求精确解，只需要做渐近估计。注意到$z\Phi(z)$在$z\geq 1.15$时就已经大于1，而我们考虑的是渐近解，所以自然可以认为满足$z_* \geq 1.15$，于是有
\begin{equation}z_* < \sqrt{2\log\frac{n-1}{\sqrt{2\pi}}}\end{equation}
将这个结果代回到方程$\eqref{eq:z}$，并利用$\Phi(z) < 1$，可以得到
\begin{equation}z_* > \sqrt{2\log\frac{n-1}{\sqrt{2\log\frac{n-1}{\sqrt{2\pi}}}\sqrt{2\pi}}}\end{equation}
由这两个上下界可以得到
\begin{equation}z_* \sim \sqrt{2\log\frac{n-1}{\sqrt{2\pi}}}\sim \sqrt{2\log\frac{n}{\sqrt{2\pi}}}\sim \sqrt{2\log n}\end{equation}
这便是我们要求的$\mathbb{E}[z_{\max}]$的渐近结果。关于这个问题的进一步探讨，可以参考Fisher–Tippett–Gnedenko theorem、Generalized extreme value distribution等内容。

逆变采样 #

最后一个证明基于逆累积分布函数的采样思路：设1维分布的累积分布函数为$\Phi(z)$，它的逆函数为$\Phi^{-1}(z)$，那么从这个分布中采样的一种方式是
\begin{equation}z = \Phi^{-1}(\varepsilon),\qquad \varepsilon\sim U(0,1)\end{equation}
即通过逆累积分布函数就可以将均匀分布转换成目标分布。那么，我们从任意目标分布采样$n$个点$z_1,z_2,\cdots,z_n$，等价于说$\Phi(z_1),\Phi(z_2),\cdots,\Phi(z_n)$是从$U(0,1)$采样出来的$n$个点。我们想要求$\mathbb{E}[z_{\max}]$，可以认为近似地成立
\begin{equation}\mathbb{E}[z_{\max}]\approx\Phi^{-1}(\mathbb{E}[\Phi(z_{\max})])\end{equation}
即在$U(0,1)$中先求相应的期望，然后再通过$\Phi^{-1}$转换回来。不难猜测，从$U(0,1)$中采样$n$个点，它们的最大值的平均值大致会是$\frac{n}{n+1}$【将区间$(0,1)$等分为$n+1$份，里边刚好有$n$个点，取最大那个】，所以有$\mathbb{E}[z_{\max}]\approx \Phi^{-1}(\frac{n}{n+1})$。这是一个通用的结果，接下来我们要结合具体的累积分布函数来得到更显式的解。

对于标准正态分布我们有$\newcommand{erf}{\mathop{\text{erf}}}\newcommand{erfc}{\mathop{\text{erfc}}}\Phi(z) = \frac{1}{2} + \frac{1}{2}\erf\left(\frac{z}{\sqrt{2}}\right) = 1 - \frac{1}{2}\erfc\left(\frac{z}{\sqrt{2}}\right)$，Erfc函数有个渐近形式$\erfc(z)\sim \frac{\exp(-z^2)}{z\sqrt{\pi}}$（可以通过分部积分推），代入到$\Phi(z)$得到
\begin{equation}\Phi(z)\sim 1 - \frac{\exp(-z^2/2)}{z\sqrt{2\pi}}\end{equation}
于是求$\Phi^{-1}(\frac{n}{n+1})$约等于解方程
\begin{equation}\frac{\exp(-z^2/2)}{z\sqrt{2\pi}} = \frac{1}{n+1}\end{equation}
这跟上一节的方程大同小异，于是根据上一节的求解过程，我们可以得到
\begin{equation}\mathbb{E}[z_{\max}] \sim \sqrt{2\log\frac{n+1}{\sqrt{2\pi}}}\sim \sqrt{2\log\frac{n}{\sqrt{2\pi}}}\sim \sqrt{2\log n}\end{equation}

应用例子 #

在文章《低精度Attention可能存在有偏的舍入误差》中，我们介绍了一种会导致低精度Attention产生计算偏差的机制，而其中一个条件是同一行Attention Logits同时存在多个最大值。这个条件容易成立吗？借助本文的结果，我们可以对出现概率做一个估计。

假设一行有$n$个Logits，它们都是从$\mathcal{N}(0,1)$中独立重复采样出来的，也可以考虑一般的均值和方差，但这并不改变后面的结论。当然，实际情况不一定是正态分布，不过这作为一个基本结果是没问题的。现在的问题是：将这$n$个Logits都转为BF16格式，那么至少出现两个相同的最大值的概率是多少？

根据前述结果，这$n$个Logits的最大值约为$\nu = \sqrt{2\log\frac{n-1}{\sqrt{2\pi}}}$，然后BF16只有7位尾数，相对精度只有$2^{-7}=1/128$，那么只要剩下的$n-1$个Logits有一个落在区间$(\frac{127}{128}\nu,\nu]$，就可以认为在BF16下出现了两个相同的最大值。根据概率密度函数的意义，单次采样落在该区间内的概率是$p(\nu)\frac{\nu}{128}$，那么$n-1$个数至少有一个落在该区间的概率是
\begin{equation}1 - \left(1 - p(\nu)\frac{\nu}{128}\right)^{n-1} = 1 - \left(1 - \frac{\nu/128}{n-1}\right)^{n-1}\approx 1 - e^{-\nu/128} \approx \frac{\nu}{128}\end{equation}
注意，当我们先确定了最大值后，剩下的$n-1$个数其实已经不能算是从标准正态分布中独立重复采样了，这里依然按独立重复采样来估算，所得结果在$n$足够大时肯定是偏小的，不过作为一个简单的近似笔者认为是可用的。

跟数值模拟结果的对比：

import jax
import jax.numpy as jnp

def proba_of_multi_max(n, T=100, seed=42):
    p, key = 0, jax.random.key(seed)
    for i in range(T):
        key, subkey = jax.random.split(key)
        logits = jax.random.normal(subkey, (10000, n)).astype('bfloat16')
        p += ((logits == logits.max(axis=1, keepdims=True)).sum(axis=1) > 1).mean()
    return p / T

def approx_result(n):
    return jnp.sqrt(2 * jnp.log(n / jnp.sqrt(2 * jnp.pi))) / 128

proba_of_multi_max(128)  # 0.018246
approx_result(128)  # 0.0219115

proba_of_multi_max(4096)  # 0.028279
approx_result(4096)  # 0.03005291

proba_of_multi_max(65536)  # 0.05296699
approx_result(65536)  # 0.03523674

可以看到，即便序列长度只有128，也约有2%的概率出现重复最大值，这非常可观，因为Flash Attention是分块计算的，每一块的经典长度就是128，每128个Logits的出现概率是2%，那么整个样本的Attention计算过程中重复最大值的平均出现次数就是$0.02\times n^2/128$这个级别（别忘了Logits矩阵大小是序列长度的平方），随便代个$n=4096$，结果都是不小的。

这里还有个小细节，就是实际Attention计算中，Logits矩阵通常不是BF16格式，而是减去$\max$再$\exp$后才转BF16，这时候最大值是1，问题等价于该矩阵每一行出现大于等于两个1的概率是多少。不过，这个细节版的结果跟直接将Logits矩阵转为BF16的结果不会有明显区别。

文章小结 #

本文用三种不同的方法估计了n个正态随机数的最大值的数学期望，并由所得结果对低精度Attention矩阵中出现重复最大值的概率做了简单估计。

转载到请包括本文地址：https://www.kexue.fm/archives/11390

更详细的转载事宜请参考：《科学空间FAQ》

打赏

微信打赏

支付宝打赏

因为网站后台对打赏并无记录，因此欢迎在打赏时候备注留言。
你还可以点击这里或在下方评论区留言来告知你的建议或需求。