生成扩散模型漫谈（三十一）：预测数据而非噪声

时至今日，LDM（Latent Diffusion Models）依旧是扩散模型的主流范式。借助Encoder对原始图像进行高倍压缩，LDM能显著减少训练与推理的计算成本，同时还能降低训难度，可谓一举多得。然而，高倍压缩也意味着信息损失，而且“压缩、生成、解压缩”的流水线也少了些端到端的美感。因此，始终有一部分人执着于“回到像素空间”，希望让扩散模型直接在原始数据上完成生成。

本文要介绍的《Back to Basics: Let Denoising Generative Models Denoise》正是这一思路的新工作，它基于原始数据往往处于低维子流形这一事实，提出模型应预测数据而不是噪声，由此得到“JiT（Just image Transformers）”，显著地简化了像素空间的扩散模型架构。

信噪之比 #

毋庸置疑，当今扩散模型的“主力军”依然是LDM，即便是前段时间颇为热闹的RAE，也只是声称LDM的Encoder已经“过时”了，要给它换一个新的更强的Encoder，但依然没改变“先压缩后生成”这一模式。

之所以有如此局面，除了因为LDM能显著降低大图生成的计算成本外，还有一个关键原因是，在相当长时间内，研究人员发现直接像素空间做高分辨率的扩散生成似乎存在一些“固有困难”，具体表现为将低分辨率下行之有效的配置（比如Noise Schedule）用于高分辨率扩散模型的训练，最终结果会明显变差，具体表现为收敛速度慢、FID不如低分辨率模型等。

后来，Simple Diffusion等工作意识到了导致这一现象的关键原因：同一Noise Schedule用到更高分辨率的图像上，其信噪比本质上是增加的。具体来说，当我们将同样强度的噪声施加到小图和大图，然后缩放到同一大小，那么大图看起来会更清晰。因此，用同样的Noise Schedule去训练高分辨率扩散模型时，去噪的难度无形之中变低了，于是带来了训练效率低下、效果不佳等问题。

意识到这个原因后，解决办法也就不难想了：调整高分辨率扩散模型的Noise Schedule，提高相应的噪声强度，以对齐每一步的信噪比即可。更详细的讨论可以参考之前的博客《生成扩散模型漫谈（二十二）：信噪比与大图生成（上）》。自此以后，像素空间中的扩散模型便逐渐追上了LDM的效果，开始体现出自己的竞争力。

模型瓶颈 #

然而，尽管在指标（如FID或IS）方面像素空间的扩散模型已经追上LDM了，但仍绕不开另一个让人困惑的问题：为了得到与低分辨率模型相近的指标，高分辨率模型必须付出更多的计算，比如更多的训练步数、更大的模型、更大的Feature Map等。

可能有读者觉得没什么：生成更大的图需要更大的成本，这不是很合理？咋看之下是有道理，但仔细想想就会发现并不科学。大图生成本质上也许更为困难，但至少对FID/IS等指标来说不应该，因为这俩指标都是将生成结果缩放到特定大小后才计算的。这意味着如果我们有一批小图，那么想要得到一批FID/IS都不变的大图是很容易的，只需要将每张小图都UpSample一下就行了，几乎零额外成本。

这时候可能会有人指出“UpSample得到的大图会缺细节啊”，没错，这就是刚才说的“大图生成本质上也许更为困难”，因为它需要生成更多的细节。但是，UpSample这个操作，至少对FID和IS是不变的。这就意味着，理论上来说，我付出同等的算力，应该至少能得到一个FID/IS都大致相同的、但细节可能不足的大图生成模型。但事实并非如此，很多时候我们只能得到一个全方面明显更糟糕的模型。

让我们来将这个问题具体化一下。假设Baseline是一个$128\times 128$的小图模型，它按$8\times 8$的Patch对输入进行Patchify，线性投影到768维，再送入一个 hidden_size=768 的ViT，最后线性投影回图片大小，这个配置在$128\times 128$分辨率上工作良好。接着我们要做的$512\times 512$的大图生成，我只需要将Patch Size改为$32\times 32$，那么除了输入输出的投影略为变大后，整体计算量几乎不变。

现在的问题是：用这样的一个计算成本大致相同的模型去训$512\times 512$的扩散模型，我们能得到跟$128\times 128$分辨率模型一样的FID/IS吗？

低维流形 #

对于JiT之前的扩散模型，答案是大概率不行，因为这样的模型在高分辨率时具有低秩瓶颈。

此前扩散模型有两种主流范式，一是像DDPM那样预测噪声，一是像ReFlow那样预测噪声与原图之差（速度），二者的回归目标都有噪声。噪声向量是独立重复地从正态分布采样出来的，它能“铺满”整个空间，用数学的话说它的支撑（Support）是全空间。这样一来，模型要想成功预测任意噪声向量，那么至少不能存在低秩瓶颈，否则连恒等映射都无法实现，更不用说去噪了。

回到刚才的例子，当Patch Size改为$32\times 32$后，输入维度是$32\times 32\times 3 = 3072$，再降维投影到768维，这自然是不可逆的，因此如果我们还是用它预测噪声或速度的话，就会因为低秩瓶颈而效果不佳。这里的关键问题是实际模型并非真的具有万能拟合能力，而是或多或少存在一些拟合瓶颈。

说到这里，其实JiT的核心改动已经呼之欲出了：

相比于噪声，原始数据的有效维度往往更低，也就是说原始数据处于一个更低维的子流形中，这意味着模型预测数据会比预测噪声更加“轻松”，因此模型应优先选择预测原始数据，尤其是网络容量有限时。

说白了，就是原始数据比如图像往往具有特定的结构，所以预测起来更简单，因此模型应该预测图像，这样可以将低秩瓶颈的影响降到最低，甚至可能将劣势转化为优势。

分开来看，这里的每一个小点都不是新的：噪声的支撑是全空间、原始数据往往处于低维流形，这些结论某种程度上已是“广为人知”；至于直接用模型预测图像而不是噪声，这也不是第一次尝试。但原论文最了不起的地方，在于把这些点同时串联起来，形成一个合理的解释，令人拍案叫绝的同时又觉得无法反驳，反而有种“本该如此”的感觉。

实验分析 #

当然，虽然看上去很合理，但到目前为止它顶多算是猜测，接下来就是通过实验来验证它。JiT里边的实验很多，但笔者认为最值得关注的是下面三个。

首先，我们现在有三个可选的预测目标，分别是噪声、速度、数据，然后它们又可以细分为模型的预测目标和损失函数的回归目标，所以一共有9种组合。以ReFlow为例，设$\boldsymbol{x}_0$是噪声，$\boldsymbol{x}_1$是数据，它的训练目标是
\begin{equation}\mathbb{E}_{\boldsymbol{x}_0\sim p_0(\boldsymbol{x}_0),\boldsymbol{x}_1\sim p_1(\boldsymbol{x}_1)}\bigg[\bigg\Vert \boldsymbol{v}_{\boldsymbol{\theta}}\big(\underbrace{(\boldsymbol{x}_1 - \boldsymbol{x}_0)t + \boldsymbol{x}_0}_{\boldsymbol{x}_t}, t\big) - (\boldsymbol{x}_1 - \boldsymbol{x}_0)\bigg\Vert^2\bigg]\end{equation}
其中$\boldsymbol{v}=\boldsymbol{x}_1 - \boldsymbol{x}_0$即速度，所以这是一个回归目标为速度的损失（$\boldsymbol{v}\text{-loss}$），如果我们用一个神经网络去建模$\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)$，那么模型的预测目标也是速度（$\boldsymbol{v}\text{-pred}$），如果我们根据$\boldsymbol{x}_1 - \boldsymbol{x}_0=\frac{\boldsymbol{x}_1 - \boldsymbol{x}_t}{1-t}$，将$\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)$参数化为$\frac{\text{NN}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t) - \boldsymbol{x}_t}{1-t}$，那么$\text{NN}$的预测目标就是数据$\boldsymbol{x}_1$（$\boldsymbol{x}\text{-pred}$）。

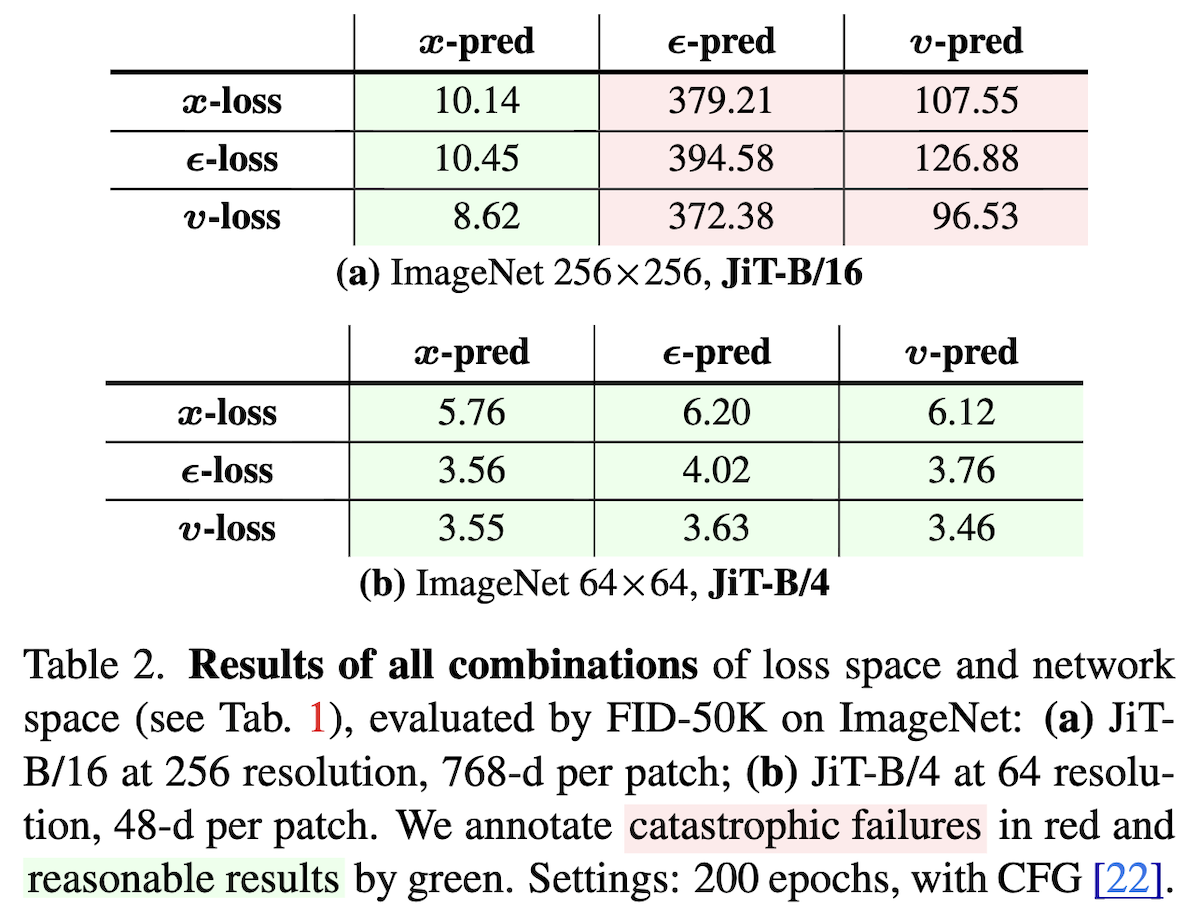
这9种组合在有/无低秩瓶颈的ViT模型上的效果分别如下图左：

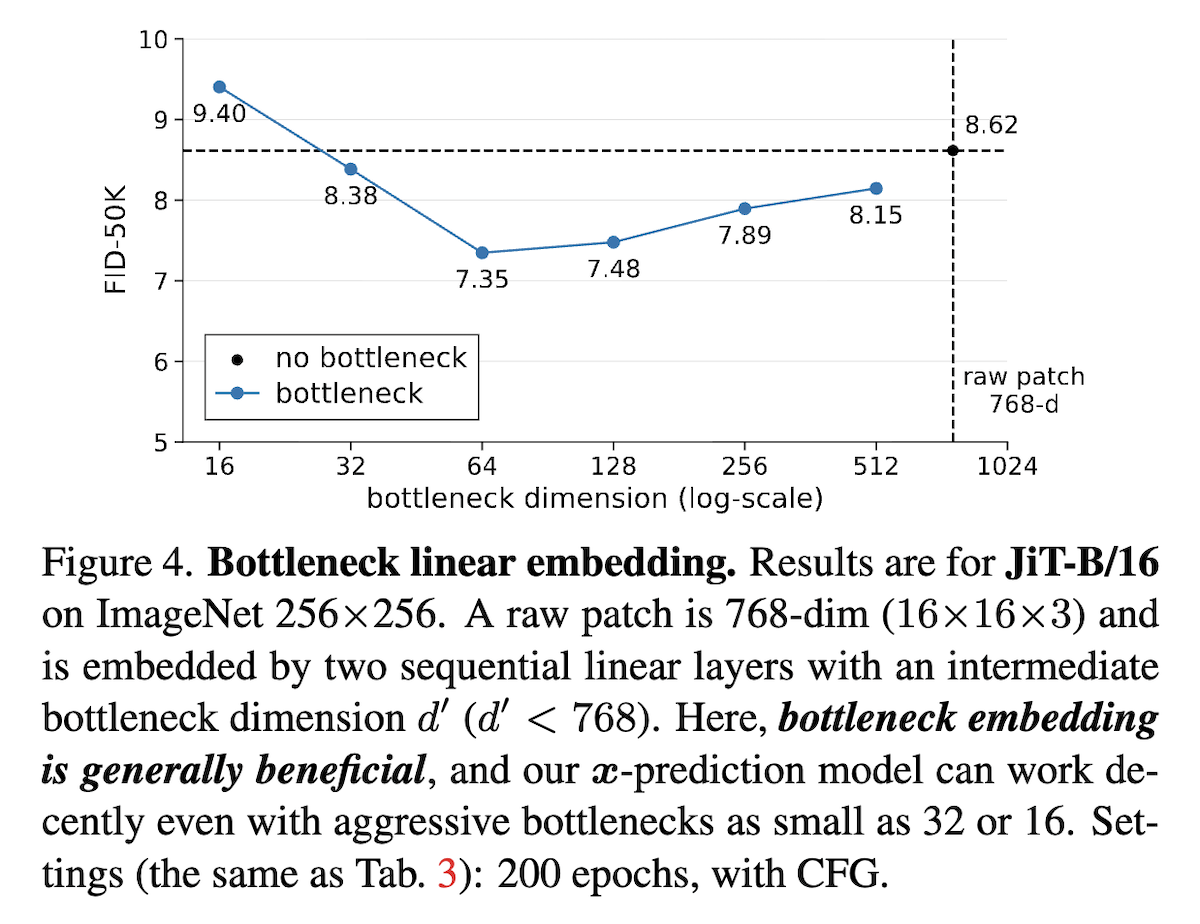
可以看到，如果没有低秩瓶颈（b），那么9种组合差别不大，但如果模型存在低秩瓶颈（a），则只有预测目标是数据（$\boldsymbol{x}\text{-pred}$）才能成功训练，至于回归目标的影响则比较次要，这就肯定了预测数据的必要性。还有，论文发现主动给$\boldsymbol{x}\text{-pred}$的JiT增加适当的低秩瓶颈，反而有利于FID，如上图右。

进一步地，下表验证了通过预测数据，确实可以在相近的计算量和参数量下，得到相近FID的不同分辨率模型：

最后，笔者也自己对比了一番，在CelebA HQ上用大Patch Size的ViT模型分别做$\boldsymbol{x}\text{-pred}$和$\boldsymbol{v}\text{-pred}$的效果对比如下（训得比较糙，对比看就行）：

延伸思考 #

更多的实验结果大家自行看原论文了，这一节我们来讨论一下，JiT给扩散模型带来了什么变化。

首先，它并没有刷新SOTA。从论文中的实验表格可以看出，就生成ImageNet图像这个任务而言，它没有带来新的SOTA，但跟最优结果的差距也不大，因此可以认为它的效果也是SOTA级别的，但总之没有明显超越它。另一方面，我们将已经是SOTA的非$\boldsymbol{x}\text{-pred}$模型改为$\boldsymbol{x}\text{-pred}$，大概率也不会得到显著更优的结果。

不过，它也许能够降低SOTA的成本。让模型预测数据，缓解了低秩瓶颈等问题的影响，使得我们可以重新审视那些曾因效果不佳而被弃用的轻量设计，或者以较低的额外训练成本，将低分辨率的SOTA模型“升级”成高分辨率模型。从这个角度看，JiT真正解决的问题是从低分辨率到高分辨率的可迁移性。

此外，JiT使得视觉理解和生成的架构更为统一。事实上，JiT基本就是视觉理解所用的ViT模型，跟文本LLM的GPT架构也大同小异，架构的统一更利于我们设计理解与生成于一体的多模态模型。相比之下，此前扩散模型的标准架构是U-Net，它包含多级上下采样和多条跨尺度直通连接，结构相对复杂。

从这个角度看，JiT可谓是准确找到了U-Net中最关键的一条直通连接。还是ReFlow的例子，如果我们按照建模$\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)$来理解，那么JiT中有$\boldsymbol{v}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)=\frac{\text{NN}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t) - \boldsymbol{x}_t}{1-t}$，额外的$-\boldsymbol{x}_t$正是从输入到输出的一条直通连接。U-Net则是不去管哪个连接关不关健，它直接给每个上/下采样的Block都加上这样一条直通连接。

最后，插个“题外话”。由JiT笔者还想到了DDCM，它需要预采样一个“$T \times \text{img_size}$”的巨大矩阵作为Codebook，笔者曾尝试用有限个随机向量的线性组合来模拟它，但以失败告终，这个经历让笔者深刻体会到独立同分布噪声是撑满整个空间的、不可压缩的。所以，当看到JiT提出“数据处于低维流形、预测数据比预测噪声更容易”观点时，笔者几乎瞬间就理解并接受了它。

文章小结 #

本文简单介绍了JiT，它基于原始数据往往处于低维子流形这一事实，提出模型应优先选择预测数据而不是噪声/速度，这样能降低扩散模型的建模难度，减少模型崩溃等负面结果的可能性。

转载到请包括本文地址：https://www.kexue.fm/archives/11428

更详细的转载事宜请参考：《科学空间FAQ》