科学空间|Scientific Spaces

时至今日，LDM（Latent Diffusion Models）依旧是扩散模型的主流范式。借助Encoder对原始图像进行高倍压缩，LDM能显著减少训练与推理的计算成本，同时还能降低训难度，可谓一举多得。然而，高倍压缩也意味着信息损失，而且“压缩、生成、解压缩”的流水线也少了些端到端的美感。因此，始终有一部分人执着于“回到像素空间”，希望让扩散模型直接在原始数据上完成生成。

本文要介绍的《Back to Basics: Let Denoising Generative Models Denoise》正是这一思路的新工作，它基于原始数据往往处于低维子流形这一事实，提出模型应预测数据而不是噪声，由此得到“JiT（Just image Transformers）”，显著地简化了像素空间的扩散模型架构。

信噪之比

毋庸置疑，当今扩散模型的“主力军”依然是LDM，即便是前段时间颇为热闹的RAE，也只是声称LDM的Encoder已经“过时”了，要给它换一个新的更强的Encoder，但依然没改变“先压缩后生成”这一模式。

点击阅读全文...

这段时间，相信很多读者已经刷到过Muon优化器的相关消息。实际上，Muon的提出时间大致是去年的10月份，由 Keller Jordan 在推特上提出，距今也不过一年多一点。然而，就在这一年里，Muon已经经历了百亿、千亿乃至万亿参数模型的训练考验，足以表明它是一个相当有竞争力的优化器。

如今，Muon已经内置在Torch、Keras等训练框架中，就连Megatron这样的大型框架也逐渐开始支持，这意味它已经获得了业界的普遍认可。不过，对于仅熟悉Adam的读者来说，如何快速有效地切换到Muon，可能依然是一件让人困惑的事情。所以，本文试图给出一个快速上手教程。

简要介绍

Muon的正式提出者是 Keller Jordan ，目前任职于OpenAI。开头说了，Muon最早发表在推特上，而直到现在，作者也只是多写了篇博客《Muon: An optimizer for hidden layers in neural networks》而不是一篇Paper，作者的观点是“是否写成Paper，跟优化器是否有效，没有任何关系^[原文]”。

点击阅读全文...

前段时间笔者在arXiv上刷到了论文《Why Low-Precision Transformer Training Fails: An Analysis on Flash Attention》，里面描述的实验现象跟我们在训练Kimi K2时出现的一些现象很吻合，比如都是第二层Attention开始出现问题。论文将其归因为低精度Attention固有的有偏误差，这个分析角度是比较出乎笔者意料的，所以饶有兴致地阅读了一番。

然而，论文的表述似乎比较让人费解——当然也有笔者本就不大熟悉低精度运算的原因。总之，经过多次向作者请教后，笔者才勉强看懂论文，遂将自己的理解记录在此，供大家参考。

结论简述

要指出的是，论文标题虽然点名了“Flash Attention”，但按照论文的描述，即便block_size取到训练长度那么大，相同的问题依然会出现，所以Flash Attention的分块计算并不是引起问题的原因，因此我们可以按照朴素的低精度Attention实现来简化分析。

点击阅读全文...

不知道大家有没有发现一个有趣的细节，Muon和MuP都是“Mu”开头，但两个“Mu”的原意完全不一样，前者是“MomentUm Orthogonalized by Newton-Schulz”，后者是“Maximal Update Parametrization”，可它们俩之间确实有着非常深刻的联系。也就是说，Muon和MuP有着截然不同的出发点，但最终都走向了相同的方向，甚至无意间取了相似的名字，似乎真应了那句“冥冥中自有安排”。

言归正传。总之，笔者在各种机缘巧合之下，刚好同时学习到了Muon和MuP，这大大加深了笔者对模型优化的理解，同时也让笔者开始思考关于模型优化更本质的原理。经过一段时间的试错，算是有些粗浅的收获，在此跟大家分享一下。

写在前面

按照提出时间的先后顺序，是先有MuP再有Muon，但笔者的学习顺序正好反过来，先学习了Muon然后再学习MuP，事后来看，这也不失为一个不错的学习顺序。

点击阅读全文...

对于坚持离散化路线的研究人员来说，VQ（Vector Quantization）是视觉理解和生成的关键部分，担任着视觉中的“Tokenizer”的角色。它提出在2017年的论文《Neural Discrete Representation Learning》，笔者在2019年的博客《VQ-VAE的简明介绍：量子化自编码器》也介绍过它。

然而，这么多年过去了，我们可以发现VQ的训练技术几乎没有变化，都是STE（Straight-Through Estimator）加额外的Aux Loss。STE倒是没啥问题，它可以说是给离散化运算设计梯度的标准方式了，但Aux Loss的存在总让人有种不够端到端的感觉，同时还引入了额外的超参要调。

幸运的是，这个局面可能要结束了，上周的论文《DiVeQ: Differentiable Vector Quantization Using the Reparameterization Trick》提出了一个新的STE技巧，它最大亮点是不需要Aux Loss，这让它显得特别简洁漂亮！

点击阅读全文...

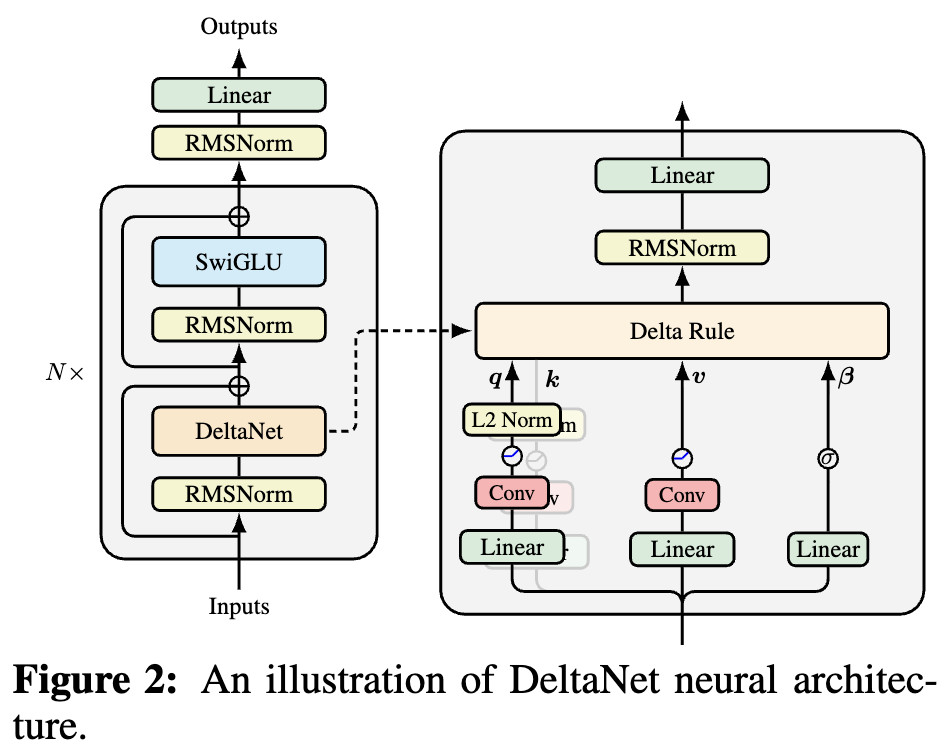
如果读者有关注模型架构方面的进展，那么就会发现，比较新的线性Attention（参考《线性注意力简史：从模仿、创新到反哺》）模型都给$\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}$加上了Short Conv，比如下图所示的DeltaNet：

DeltaNet中的Short Conv

为什么要加这个Short Conv呢？直观理解可能是增加模型深度、增强模型的Token-Mixing能力等，说白了就是补偿线性化导致的表达能力下降。这个说法当然是大差不差，但它属于“万能模版”式的回答，我们更想对它的生效机制有更准确的认知。

接下来，笔者将给出自己的一个理解（更准确说应该是猜测）。

点击阅读全文...

很早之前就有读者提出希望可以给Cool Papers增加导入Zotero的功能，但由于笔者没用Zotero，加上又比较懒，所以一直没提上日程。这个周末刚好有点时间，研究了一下，做了个简单的适配。

单篇导入

首先，我们需要安装Zotero（这是废话），然后需要给所用浏览器安装Zotero Connector插件。安装完成后，我们访问Cool Papers的单篇论文页面，如 https://papers.cool/arxiv/2104.09864 或 https://papers.cool/venue/2024.naacl-long.431@ACL ，然后点击Zotero Connector的图标，就会自动把论文导入了，包括PDF文件。

单篇论文导入到Zotero

点击阅读全文...

前段时间搞了个很迷你的开发板树莓派Zero2W（下面简称“Pi”），还搭配了个USB Key转接板，这几天折腾了一下，用于实现一个随身的旁路由。本文记录一下关键技术点，供有同样需求的读者参考。

树莓派Zero2W

点击阅读全文...