Transformer升级之路：18、RoPE的底数选择原则

我们知道，在RoPE中频率的计算公式为$\theta_i = b^{-2i/d}$，底数$b$默认值为10000。目前Long Context的主流做法之一是，先在$b=10000$上用短文本预训练，然后调大$b$并在长文本微调，其出发点是《Transformer升级之路：10、RoPE是一种β进制编码》里介绍的NTK-RoPE，它本身有较好长度外推性，换用更大的$b$再微调相比不加改动的微调，起始损失更小，收敛也更快。该过程给人的感觉是：调大$b$完全是因为“先短后长”的训练策略，如果一直都用长文本训练似乎就没必要调大$b$了？

上周的论文《Base of RoPE Bounds Context Length》试图回答这个问题，它基于一个期望性质研究了$b$的下界，由此指出更大的训练长度本身就应该选择更大的底数，与训练策略无关。整个分析思路颇有启发性，接下来我们一起来品鉴一番。

期望性质 #

RoPE这里就不再详细介绍了，它本质上是一个分块对角矩阵
\begin{equation}\boldsymbol{\mathcal{R}}_n = \scriptsize{\left(\begin{array}{cc:cc:cc:cc}
\cos n\theta_0 & -\sin n\theta_0 & 0 & 0 & \cdots & \cdots & 0 & 0 \\
\sin n\theta_0 & \cos n\theta_0 & 0 & 0 & \cdots & \cdots & 0 & 0 \\
\hdashline
0 & 0 & \cos n\theta_1 & -\sin n\theta_1 & \cdots & \cdots & 0 & 0 \\
0 & 0 & \sin n\theta_1 & \cos n\theta_1 & \cdots & \cdots & 0 & 0 \\
\hdashline
\vdots & \vdots & \vdots & \vdots & \ddots & \ddots & \vdots & \vdots \\
\vdots & \vdots & \vdots & \vdots & \ddots & \ddots & \vdots & \vdots \\
\hdashline
0 & 0 & 0 & 0 & \cdots & \cdots & \cos n\theta_{d/2-1} & -\sin n\theta_{d/2-1} \\
0 & 0 & 0 & 0 & \cdots & \cdots & \sin n\theta_{d/2-1} & \cos n\theta_{d/2-1} \\
\end{array}\right)}\end{equation}
然后利用恒等式
\begin{equation}(\boldsymbol{\mathcal{R}}_m \boldsymbol{q})^{\top}(\boldsymbol{\mathcal{R}}_n \boldsymbol{k}) = \boldsymbol{q}^{\top} \boldsymbol{\mathcal{R}}_m^{\top}\boldsymbol{\mathcal{R}}_n \boldsymbol{k} = \boldsymbol{q}^{\top} \boldsymbol{\mathcal{R}}_{n-m} \boldsymbol{k}\end{equation}
给$\boldsymbol{q},\boldsymbol{k}$注入绝对位置信息，并自动实现了相对位置的效果。其中$\theta_i = b^{-2i/d}$，这里的$b$的取值就是本文要探讨的问题。

除了给模型注入位置信息外，我们期望RoPE能具备两个理想性质，以达到更好的效果：1、远程衰减，即位置相近的Token平均来说获得更多的注意力；2、语义聚合，即语义相似的Token平均来说获得更多的注意力。其中第一点我们早在《Transformer升级之路：2、博采众长的旋转式位置编码》有过相关讨论，RoPE确实有一定的远程衰减性质。

所以接下来我们来分析第二点。

不等关系 #

所谓语义聚合，指的是当$\boldsymbol{k}$与$\boldsymbol{q}$相近时，不管它们的相对距离$n-m$多大，其注意力$\boldsymbol{q}^{\top} \boldsymbol{\mathcal{R}}_{n-m} \boldsymbol{k}$平均来说都应该更大（至少要比随机的两个Token更大）。为了得到一个量化的结论，我们进一步简化问题，假设$\boldsymbol{q}$的每个分量都是独立同分布的，每个分量的均值为$\mu$，方差为$\sigma^2$。

现在我们考虑两种不同的$\boldsymbol{k}$：一种是在$\boldsymbol{q}$的基础上，加上一个零均值的扰动$\boldsymbol{\varepsilon}$，我们记$\tilde{\boldsymbol{k}} = \boldsymbol{q} + \boldsymbol{\varepsilon}$，代表跟$\boldsymbol{q}$语义相近的Token；另一种则是假设$\boldsymbol{k}$跟$\boldsymbol{q}$独立同分布，这代表两个随机的Token。根据第二点理想性质，我们希望有
\begin{equation}\mathbb{E}_{\boldsymbol{q},\boldsymbol{k},\boldsymbol{\varepsilon}}\big[\boldsymbol{q}^{\top} \boldsymbol{\mathcal{R}}_{n-m} \tilde{\boldsymbol{k}} - \boldsymbol{q}^{\top} \boldsymbol{\mathcal{R}}_{n-m} \boldsymbol{k}\big] \geq 0\end{equation}
注意我们刚才反复强调了“平均来说”，意味着我们只是期望一个平均的趋势，而不是每一点都能严格成立，所以我们在上式加了取数学期望$\mathbb{E}_{\boldsymbol{q},\boldsymbol{k},\boldsymbol{\varepsilon}}$。现在根据假设和RoPE的定义，我们可以把上式具体地算出来：
\begin{equation}\begin{aligned}
&\,\mathbb{E}_{\boldsymbol{q},\boldsymbol{k},\boldsymbol{\varepsilon}}\big[\boldsymbol{q}^{\top} \boldsymbol{\mathcal{R}}_{n-m} (\boldsymbol{q} + \boldsymbol{\varepsilon}) - \boldsymbol{q}^{\top} \boldsymbol{\mathcal{R}}_{n-m} \boldsymbol{k}\big] \\[5pt]
=&\, \mathbb{E}_{\boldsymbol{q}}\big[\boldsymbol{q}^{\top} \boldsymbol{\mathcal{R}}_{n-m} \boldsymbol{q}\big] - \mathbb{E}_{\boldsymbol{q},\boldsymbol{k}}\big[\boldsymbol{q}^{\top} \boldsymbol{\mathcal{R}}_{n-m} \boldsymbol{k}\big] \\[5pt]
=&\, \mathbb{E}_{\boldsymbol{q}}\big[\boldsymbol{q}^{\top} \boldsymbol{\mathcal{R}}_{n-m} \boldsymbol{q}\big] - \mathbb{E}_{\boldsymbol{q}}[\boldsymbol{q}]^{\top}\boldsymbol{\mathcal{R}}_{n-m} \mathbb{E}_{\boldsymbol{k}}[\boldsymbol{k}] \\[5pt]
=&\, \mathbb{E}_{\boldsymbol{q}}\big[\boldsymbol{q}^{\top} \boldsymbol{\mathcal{R}}_{n-m} \boldsymbol{q}\big] - \mu^2\boldsymbol{1}^{\top}\boldsymbol{\mathcal{R}}_{n-m} \boldsymbol{1} \\[5pt]
=& \mathbb{E}_{\boldsymbol{q}}\left[\sum_{i=0}^{d/2-1} (q_{2i}^2 + q_{2i+1}^2)\cos (n-m)\theta_i\right] - \sum_{i=0}^{d/2-1} 2\mu^2\cos (n-m)\theta_i \\[5pt]
=& \sum_{i=0}^{d/2-1} 2(\mu^2 + \sigma^2)\cos (n-m)\theta_i - \sum_{i=0}^{d/2-1} 2\mu^2\cos (n-m)\theta_i \\[5pt]
=& \sum_{i=0}^{d/2-1} 2\sigma^2\cos (n-m)\theta_i \\
\end{aligned}\end{equation}
如果训练长度最大为$L$，那么$n-m\leq L-1$，因此第二点理想性质可以用如下不等式近似描述：
\begin{equation}\sum_{i=0}^{d/2-1} \cos m\theta_i \geq 0,\quad m\in\{0,1,2,\cdots,L-1\}\label{neq:base}\end{equation}
其中$L$是最大长度，是训练前就要选定的超参，而$d$是模型的head_size，按照LLAMA的一般设置是$d=128$，这也就意味着，上式的唯一可调参数就是$\theta_i = b^{-2i/d}$中的$b$。在《Transformer升级之路：1、Sinusoidal位置编码追根溯源》中我们就简单探究过这个函数，它整体趋势是衰减的，$b$越大则衰减速度越慢，对应的连续非负区间就越大，所以存在一个最小的$b$使得上述不等式恒成立，即
\begin{equation}b^* = \inf\left\{\,\,b\,\,\,\left|\,\,\,f_b(m)\triangleq\sum_{i=0}^{d/2-1} \cos m b^{-2i/d} \geq 0,\,\, m\in\{0,1,2,\cdots,L-1\}\right.\right\}\end{equation}

数值求解 #

由于$f_b(m)$涉及到多个三角函数的求和，并且$\theta_i$关于$i$还是非线性的，很难想象上述问题会有解析解，因此只能诉诸数值求解了。然而，$f_b(m)$越到后面震荡越频繁且不规律，因此即便数值求解也不是那么简单的事情。

笔者一开始以为，如果$b_0$使得$f_{b_0}(m)\geq 0$恒成立，那么$\forall b \geq b_0$都恒成立$f_b(m)\geq 0$，所以用二分法就可以了。但事实上这个假设并不成立，所以二分法宣告破产。继续想了一段时间，依然没什么优化思路，期间向原论文作者请教过，他们采用的是逆函数法，即给定$b$求使得$f_b(m)\geq 0$恒成立的最大$L$是比较简单的，于是我们可以得到很多$(b, L)$对，理论上只要枚举的$b$足够多，那么对于任意$L$都可以找出最小的$b$。然而这里有个精度问题，原论文最大的$L$计算到了$10^6$，$b$至少要枚举到$10^8$，如果枚举间隔小，那么计算成本非常大，如果枚举间隔大，那么可能漏掉很多解。

最后，笔者决定还是用“Jax + GPU”进行暴力搜索，以求得到更高精度的结果，大致流程是：

1、初始化$b=1000L$（在$10^6$内$b=1000L$可以使得$f_b(m)\geq 0$恒成立）；

2、遍历$k=1,2,3,4,5$，执行以下操作：

  2.1）将$[0,b]$等分为$10^k$份，遍历等分点，判断$f_b(m)\geq 0$是否恒成立；

  2.2）取最小的使得$f_b(m)\geq 0$恒成立的等分点，更新$b$；

3、返回最终的$b$。

最终结果普遍要比原论文的更紧一些
$$\scriptsize\begin{array}{c|cccccccccc}
\hline
L & 1k & 2k & 4k & 8k & 16k & 32k & 64k & 128k & 256k & 512k & 1M \\
\hline
b^*(\text{原文}) & 4.3e3 & 1.6e4 & 2.7e4 & 8.4e4 & 3.1e5 & 6.4e5 & 2.1e6 & 7.8e6 & 3.6e7 & 6.4e7 & 5.1e8 \\
b^*(\text{本文}) & 4.3e3 & \color{red}{1.2e4} & 2.7e4 & 8.4e4 & \color{red}{2.3e5} & \color{red}{6.3e5} & 2.1e6 & \color{red}{4.9e6} & \color{red}{2.4e7} & \color{red}{5.8e7} & \color{red}{6.5e7} \\
\hline
\end{array}$$

参考代码：

from functools import partial
import numpy as np
import jax.numpy as jnp
import jax

@partial(jax.jit, static_argnums=(2,))
def f(m, b, d=128):
    i = jnp.arange(d / 2)
    return jnp.cos(m[:, None] * b ** (-2 * i[None] / d)).sum(axis=1)

@np.vectorize
def fmin(L, b):
    return f(np.arange(L), b).min()

def bmin(L):
    B = 1000 * L
    for k in range(1, 6):
        bs = np.linspace(0, 1, 10**k + 1)[1:] * B  
        ys = fmin(L, bs)
        for b, y in zip(bs, ys):
            if y >= 0:
                B = b
                break
    return B

bmin(1024 * 128)

渐近估计 #

除了数值求解外，我们也可以通过渐近分析来得到一个解析的估计结果，这个估计比数值结果要小，本质上是$d\to\infty$的解，但同样能够得出“$b$应该随着$L$增大而增大”的结论。

渐近估计的思路，是用积分代替求和：
\begin{equation}f_b(m) = \sum_{i=0}^{d/2-1} \cos m b^{-2i/d}\approx \int_0^1 \cos m b^{-s} ds \xlongequal{\text{令}t = mb^{-s}} \int_{mb^{-1}}^m \frac{\cos t}{t \ln b}dt\end{equation}
其中我们记
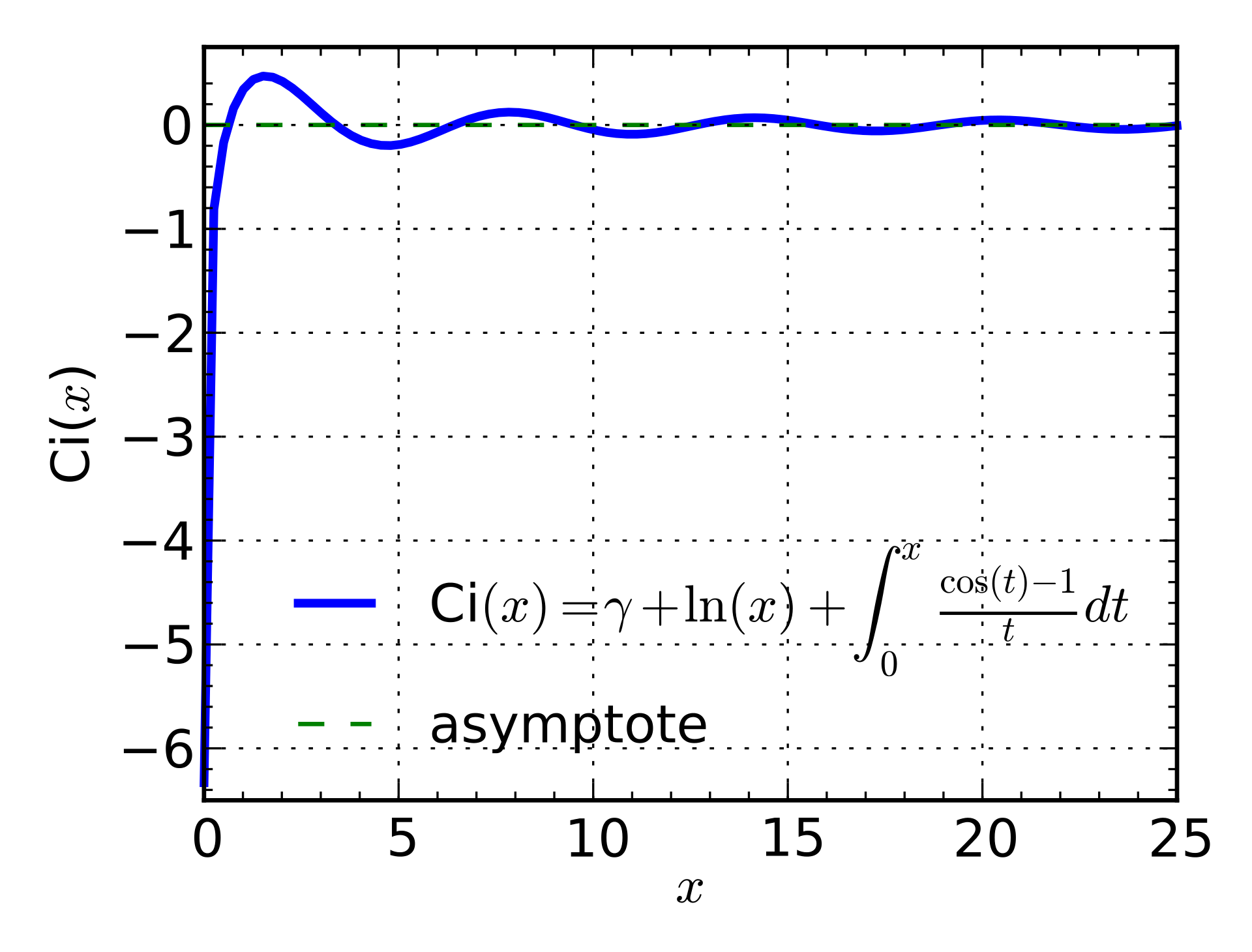
\begin{equation}\text{Ci}(x) = -\int_x^{\infty} \frac{\cos t}{t} dt\end{equation}
这是被前人研究过的三角积分（参考 Trigonometric integral ），利用这个记号，我们可以写出
\begin{equation}f_b(m) \approx \frac{\text{Ci}(m) - \text{Ci}(mb^{-1})}{\ln b}\end{equation}
$\text{Ci}(x)$的图像长这样：

它的第一个零点是$x_0=0.6165\cdots$，对于$m\geq 1$，可以看出$|\text{Ci}(m)|\leq 1/2$，所以其实$\text{Ci}(m)$相对来说是小项，对于渐近估计来说可以忽略，那么问题近似地变成了$\text{Ci}(mb^{-1})\leq 0$对于$m=1,2,\cdots,L$恒成立，我们只需要让相应的$mb^{-1}$都落在$[0,x_0]$区间内就可以实现，这意味着$Lb^{-1}\leq x_0$，即
\begin{equation}b \geq L / x_0 \approx 2L\end{equation}
或者简单点$b^* = \mathcal{O}(L)$。不出意料这个结果比精确的数值结果要小，因为它对应于$d\to\infty$，无限个三角函数叠加会使得函数图像的震荡更少，看起来更加平稳（相比于有限的$d$），从而对于固定的$b$，$f_b(m)$的连续非负区间更长，或者反过来，对于固定的$L$，保持$m=0,1,2,\cdots,L-1$的$f_b(m)$都非负的$b$更小。

相关思考 #

在《Transformer升级之路：10、RoPE是一种β进制编码》中，我们将RoPE类比为一种$\beta$进制表示，其中$\beta = b^{2/d}$，那么$b - 1= \beta^{d/2} - 1$正好是$d/2$位$\beta$进制编码能够表示的最大数字，于是要表示$0,1,2,\cdots,L-1$这$L$个位置编码，至少有$b \geq L$，这个朴素的类比再次给出了“$b$应该随着$L$增大而增大”的结论，其结果跟上一节的渐近分析结果更为接近。

另一方面，Meta最新发布的LLAMA3，训练长度为8192，但RoPE的底数选择了惊人的500000（5e5），这比前面的数值结果（8.4e4）还要大将近一个数量级，不管从哪个角度看，这个数值笔者都认为是偏大的，可能LLAMA3的这个底数本就是给更大文本长度预留的。但不论如何，更大的文本长度选择更大的RoPE底数，似乎已经成为了很多训练人员的共识。

其实不管是数值结果还是渐近估计，都只是一个参考值，实际上对于给定的$L$，一个相当大范围内的$b$都应该会有相近的效果。所以具体的数值都不重要，关键是原论文通过语义聚合的出发点和一系列推导，澄清了“$b$应该随着$L$增大而增大”的结论及其原理，这是笔者所认为的原论文的核心贡献。

此外，其实语义聚合的出发点和结论也可以用来解释Position Interpolation（PI）。刚才我们说了，同一个$b$，$f_b(m)$的连续非负区间是固定的，如果要使$0,1,2,\cdots,L-1$都落在非负区间内，就需要随着$L$的增大而相应的增加$b$。但反过来，我们也可以不增加$b$，而是减少相邻位置的间隔（即位置ID改成$0,1/k,2/k,\cdots$），那么就可以在同样大小的非负区间内表示$k$倍的位置了，这便是语义聚合视角下的Position Interpolation。

部分旋转 #

RoPE提出于2021年，当时只有一篇中文博客，后来得到了EleutherAI组织的认可和实验，继而才逐渐向学术界推广。当时EleutherAI实验发现，如果只对部分维度加RoPE，会取得稍优的结果，相关内容可以参考这里、这里和这里，后来这个操作用到了它们的GPT-NeoX中。

当然，部分旋转还不是当前LLM的主流选择，但这不妨碍我们研究它，也许它未成为主流选择只是因为我们对它还不够了解。那为什么部分旋转反而可能会更优呢？笔者发现可以用本文的结论来一定程度上解释它。以只旋转一半维度为例，它在数学上等价于选择如下的$\theta_i$：
\begin{equation}\theta_i = \left\{\begin{aligned}&b^{-4i/d},& i < d/4 \\
&0,&i \geq d/4\end{aligned}\right.\end{equation}
此时我们有
\begin{equation}\sum_{i=0}^{d/2-1} \cos m\theta_i = \sum_{i=0}^{d/4-1} (1+\cos mb^{-4i/d})\geq 0\end{equation}
也就是不论$m,b$如何，我们所期望的不等式$\eqref{neq:base}$都自动成立，这意味着从本文的观点来看，部分旋转在赋予位置信息的同时有更好的语义聚合能力，这对模型的效果也许更加有利。同时，部分旋转对模型的长文本能力或许也更有利，因为不等式恒成立，所以按照本文的观点，不论长短文本训练都不用修改$b$。

值得一提的是，DeepSeek提出的MLA也应用了部分旋转，虽然在MLA的原始推导中，部分旋转更多是为了整合RoPE的无奈之举，但结合以往的部分旋转实验结果来看，也许MLA的优异效果有部分旋转的一分功劳。

文章小结 #

本文简单介绍了论文《Base of RoPE Bounds Context Length》，它从语义聚合的期望性质讨论了RoPE的底数下界，由此指出更大的训练长度应该选择更大的底数，而不单单是为了配合“先短后长”的训练策略、继而利用NTK-RoPE来降低初始损失的折中选择。

转载到请包括本文地址：https://kexue.fm/archives/10122

更详细的转载事宜请参考：《科学空间FAQ》