滑动平均视角下的权重衰减和学习率

权重衰减（Weight Decay）和学习率（Learning Rate）是LLM预训练的重要组成部分，它们的设置是否妥当，是模型最终成败的关键因素之一。自AdamW以来，单独分离出Weight Decay来取代传统的L2正则，基本上已经成为了共识，但在此基础上，如何合理地设置Weight Decay和Learning Rate，并没有显著的理论进展。

本文将抛砖引玉，分享笔者关于这个问题的一些新理解：把训练过程看作对训练数据的滑动平均记忆，探讨如何设置Weight Decay和Learning Rate才能让这个记忆更为科学。

滑动平均 #

Weight Decay的一般形式是
\begin{equation}\boldsymbol{\theta}_t = \boldsymbol{\theta}_{t-1} - \eta_t (\boldsymbol{u}_t + \lambda_t \boldsymbol{\theta}_{t-1})\end{equation}
其中$\boldsymbol{\theta}$是参数，$\boldsymbol{u}$是优化器给出的更新量，$\lambda_t,\eta_t$亦即我们说的Weight Decay和Learning Rate，而整个序列$\{\lambda_t\}$和$\{\eta_t\}$，我们分别称为“WD Schedule”和“LR Schedule”。引入记号
\begin{equation}\begin{aligned}
\boldsymbol{m}_t =&\, \beta_1 \boldsymbol{m}_{t-1} + \left(1 - \beta_1\right) \boldsymbol{g}_t, & \hat{\boldsymbol{m}}_t =&\, \boldsymbol{m}_t\left/\left(1 - \beta_1^t\right)\right. &\\[5pt]
\boldsymbol{v}_t =&\, \beta_2 \boldsymbol{v}_{t-1} + \left(1 - \beta_2\right) \boldsymbol{g}_t^2,& \hat{\boldsymbol{v}}_t =&\, \boldsymbol{v}_t\left/\left(1 - \beta_2^t\right)\right. &
\end{aligned}\end{equation}
那么对于SGDM来说有$\boldsymbol{u}_t=\boldsymbol{m}_t$，对于RMSProp来说$\boldsymbol{u}_t= \boldsymbol{g}_t/(\sqrt{\boldsymbol{v}_t} + \epsilon)$，对于Adam来说则是$\boldsymbol{u}_t=\hat{\boldsymbol{m}}_t\left/\left(\sqrt{\hat{\boldsymbol{v}}_t} + \epsilon\right)\right.$，对于SignSGDM来说则$\newcommand{sign}{\mathop{\text{sign}}}\boldsymbol{u}_t=\sign(\boldsymbol{m}_t)$，而Muon则是$\newcommand{msign}{\mathop{\text{msign}}}\boldsymbol{u}_t=\msign(\boldsymbol{m}_t)$。这里列举的例子，除了SGDM外，其他都算是某种自适应学习率优化器。

我们的出发点是滑动平均（Exponential Moving Average，EMA）视角，即将Weight Decay写成
\begin{equation}\boldsymbol{\theta}_t = (1 - \lambda_t \eta_t)\boldsymbol{\theta}_{t-1} - \eta_t \boldsymbol{u}_t = (1 - \lambda_t \eta_t)\boldsymbol{\theta}_{t-1} + \lambda_t \eta_t ( -\boldsymbol{u}_t / \lambda_t)\label{eq:wd-ema}\end{equation}
此时Weight Decay表现为模型参数与$-\boldsymbol{u}_t / \lambda_t$的加权平均形式。滑动平均视角不是新的，《How to set AdamW's weight decay as you scale model and dataset size》、《Power Lines: Scaling Laws for Weight Decay and Batch Size in LLM Pre-training》等文章已有过讨论，本文则是在这个视角下将各方面算得更仔细一些。

接下来的篇幅我们主要以Adam为例，最后再讨论其他优化器的可用性。计算过程跟《AdamW的Weight RMS的渐近估计（上）》和《AdamW的Weight RMS的渐近估计（下）》会有相当一部份重叠之处，读者可以相互参考着阅读。

迭代展开 #

简单起见，我们先考虑常数$\lambda,\eta$，记$\beta_3 = 1 - \lambda\eta$，那么$\boldsymbol{\theta}_t = \beta_3 \boldsymbol{\theta}_{t-1} + (1 - \beta_3)( -\boldsymbol{u}_t / \lambda)$，这样形式上就跟$\boldsymbol{m}_t,\boldsymbol{v}_t$一致了。直接迭代展开得
\begin{equation}\boldsymbol{\theta}_t = \beta_3^t \boldsymbol{\theta}_0 + (1 - \beta_3)\sum_{i=1}^t \beta_3^{t-i} (-\boldsymbol{u}_i / \lambda) \end{equation}
对于Adam有$\boldsymbol{u}_t=\hat{\boldsymbol{m}}_t\left/\left(\sqrt{\hat{\boldsymbol{v}}_t} + \epsilon\right)\right.$，一般在训练结束时，$t$都能足够大以至于$\beta_1^t,\beta_2^t$足够接近于零，所以可以不去区分$\boldsymbol{m}_t$和$\hat{\boldsymbol{m}}_t$、$\boldsymbol{v}_t$和$\hat{\boldsymbol{v}}_t$，进一步地，简单设$\epsilon=0$，那么可以简化成$\boldsymbol{u}_t=\boldsymbol{m}_t / \sqrt{\boldsymbol{v}_t}$，然后来个经典的平均场近似
\begin{equation}\underbrace{\frac{1-\beta_3}{1-\beta_3^t}\sum_{i=1}^t \beta_3^{t-i} \boldsymbol{u}_i}_{\text{记为}\bar{\boldsymbol{u}}_t} = \frac{1-\beta_3}{1-\beta_3^t}\sum_{i=1}^t \beta_3^{t-i} \frac{\boldsymbol{m}_i}{\sqrt{\boldsymbol{v}_i}}\approx \frac{\bar{\boldsymbol{m}}_t \,\,\triangleq\,\, \frac{1-\beta_3}{1-\beta_3^t}\sum_{i=1}^t \beta_3^{t-i}\boldsymbol{m}_i}{\sqrt{\bar{\boldsymbol{v}}_t \,\,\triangleq\,\, \frac{1-\beta_3}{1-\beta_3^t}\sum_{i=1}^t \beta_3^{t-i}\boldsymbol{v}_i}}\label{eq:u-bar}\end{equation}
展开$\boldsymbol{m}_t,\boldsymbol{v}_t$得$\boldsymbol{m}_t = (1 - \beta_1)\sum_{i=1}^t \beta_1^{t-i}\boldsymbol{g}_i$和$\boldsymbol{v}_t = (1 - \beta_2)\sum_{i=1}^t \beta_2^{t-i}\boldsymbol{g}_i^2$，代入上式
\begin{gather}
\bar{\boldsymbol{m}}_t = \frac{(1-\beta_3)(1 - \beta_1)}{1-\beta_3^t}\sum_{i=1}^t \beta_3^{t-i} \sum_{j=1}^i \beta_1^{i-j}\boldsymbol{g}_j = \frac{(1-\beta_3)(1 - \beta_1)}{(1-\beta_3^t)(\beta_3 - \beta_1)}\sum_{j=1}^t (\beta_3^{t-j+1} - \beta_1^{t-j+1})\boldsymbol{g}_j\\[6pt]
\bar{\boldsymbol{v}}_t = \frac{(1-\beta_3)(1 - \beta_2)}{1-\beta_3^t}\sum_{i=1}^t \beta_3^{t-i} \sum_{j=1}^i \beta_2^{i-j}\boldsymbol{g}_j^2 = \frac{(1-\beta_3)(1 - \beta_2)}{(1-\beta_3^t)(\beta_3 - \beta_2)}\sum_{j=1}^t (\beta_3^{t-j+1} - \beta_2^{t-j+1})\boldsymbol{g}_j^2
\end{gather}
交换求和符号基于恒等式$\sum_{i=1}^t \sum_{j=1}^i a_i b_j = \sum_{j=1}^t \sum_{i=j}^t a_i b_j$。综上，我们有
\begin{equation}\boldsymbol{\theta}_t = \beta_3^t \boldsymbol{\theta}_0 + (1 - \beta_3^t)(-\bar{\boldsymbol{u}}_t / \lambda) \label{eq:theta-0-bar-u}\end{equation}
权重$\boldsymbol{\theta}_t$是我们想要的训练结果，它被表示为$\boldsymbol{\theta}_0$和$-\bar{\boldsymbol{u}}_t / \lambda$的加权平均。其中，$\boldsymbol{\theta}_0$是初始权重，$\bar{\boldsymbol{u}}_t$则是数据相关的，在平均场近似下它约等于$\bar{\boldsymbol{m}}_t/\sqrt{\bar{\boldsymbol{v}}_t}$，而$\bar{\boldsymbol{m}}_t$和$\bar{\boldsymbol{v}}_t$可以表示成每一步梯度的加权求和，以$\bar{\boldsymbol{m}}_t$为例，第$j$步的梯度权重正比于$\beta_3^{t-j+1} - \beta_1^{t-j+1}$。

记忆周期 #

我们主要关心的是预训练，特点是Single-Epoch，大部分数据都只过一遍，所以训出好效果的关键之一是不要忘掉早期的数据。假设训练数据已经经过全局打乱，那么可以合理地认为每一个Batch的数据都同等重要。

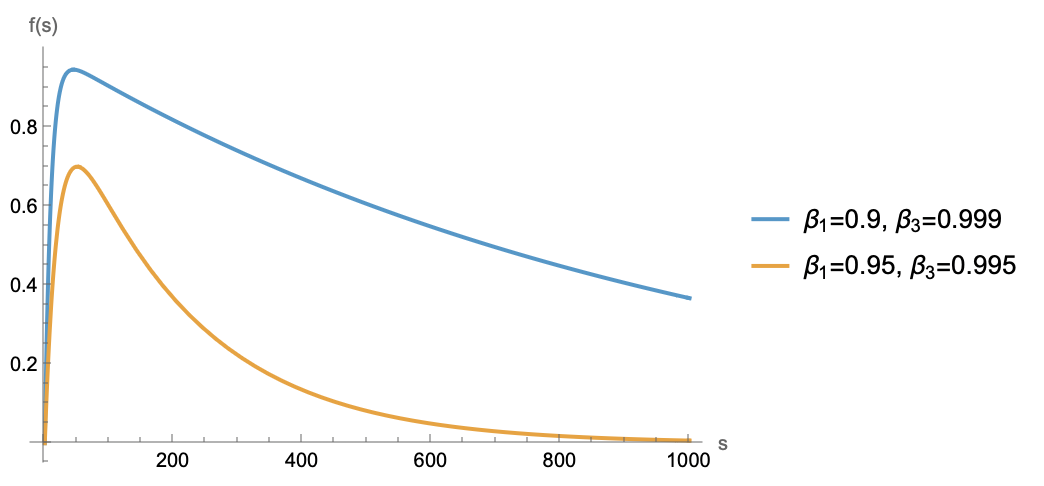
数据是以梯度形式线性叠加到$\bar{\boldsymbol{m}}_t$中的，假设每一步梯度只包含当前Batch的信息，那么某个Batch想要不被遗忘，系数$\beta_3^{t-j+1} - \beta_1^{t-j+1}$就不能太小。考察函数$f(s) = \beta_3^s - \beta_1^s$，它是一个先增后减的函数，但因为$\beta_3$会比$\beta_1$更接近于1，所以增的步数不多，远处更多是接近指数下降，如下图：

总之趋势是距离越远系数越小。那么要想模型不遗忘每一个Batch，最远处的系数就不能太小。假设系数不小于$c \in (0, 1)$才能被记住，当$s$足够大时$\beta_1^s$先趋于0，所以$\beta_3^s - \beta_1^s\approx \beta_3^s$，由$\beta_3^s\geq c$解得$s \leq \frac{\log c}{\log \beta_3} \approx \frac{-\log c}{\lambda\eta}$。这表明，模型顶多能记住$\mathcal{O}(1/\lambda\eta)$步的数据，这是它的记忆周期。

那直接无脑$\lambda=0$，让记忆周期无限大，是否就可以不担心遗忘问题了？理论上是的，然而这并不是一个好选择。Weight Decay还有一个作用是帮助模型忘掉初始化。由式$\eqref{eq:theta-0-bar-u}$可知初始化$\boldsymbol{\theta}_0$的权重是$\beta_3^t$，如果$\beta_3$太大或者训练步数$t$太小，那么初始化的占比还很高，模型可能还处于欠拟合阶段。

此外，Weight Decay还有利于稳定模型“内科”。在《AdamW的Weight RMS的渐近估计（上）》我们已经推导过，AdamW的Weight RMS的渐近结果是$\sqrt{\eta/2\lambda}$，如果$\lambda=0$，那么Weight RMS会以$\eta\sqrt{t}$的速率膨胀。这意味着直接设置$\lambda=0$，还可能带来权重爆炸等模型内科异常。

因此，$\beta_3$不能太小，以免忘记早期数据，同时也不能太大，以免欠拟合或者权重爆炸。比较适合的设置是让$1/\lambda\eta$正比于训练步数，如果是Multi-Epoch的训练场景，则考虑让$1/\lambda\eta$正比于单个Epoch的训练步数。

动态版本 #

在实际训练中，我们更多是适用动态变化的LR Schedule，比如Consine Decay、Linear Decay、WSD（Warmup-Stable-Decay）等，所以上述静态Weight Decay和Learning Rate的结果并不完全符合实践，我们需要将它们推广到动态版。

从式$\eqref{eq:wd-ema}$出发，利用近似$1 - \lambda_t \eta_t\approx e^{-\lambda_t \eta_t}$，并迭代展开，可得
\begin{equation}\boldsymbol{\theta}_t = (1 - \lambda_t \eta_t)\boldsymbol{\theta}_{t-1} - \eta_t \boldsymbol{u}_t \approx e^{-\lambda_t \eta_t}\boldsymbol{\theta}_{t-1} - \eta_t \boldsymbol{u}_t = e^{-\kappa_t}\left(\boldsymbol{\theta}_0 - \sum_{i=1}^t e^{\kappa_i}\eta_i\boldsymbol{u}_i\right)\end{equation}
其中$\kappa_t = \sum_{i=1}^t \eta_i\lambda_i$。继续设$z_t = \sum_{i=1}^t e^{\kappa_i}\eta_i$，那么可以得到同样的平均场近似
\begin{equation}\bar{\boldsymbol{u}}_t\triangleq\frac{1}{z_t}\sum_{i=1}^t e^{\kappa_i}\eta_i \boldsymbol{u}_i = \frac{1}{z_t}\sum_{i=1}^t e^{\kappa_i}\eta_i \frac{\boldsymbol{m}_i}{\sqrt{\boldsymbol{v}_i}}\approx \frac{\bar{\boldsymbol{m}}_t \,\,\triangleq\,\, \frac{1}{z_t}\sum_{i=1}^t e^{\kappa_i}\eta_i\boldsymbol{m}_i}{\sqrt{\bar{\boldsymbol{v}}_t \,\,\triangleq\,\, \frac{1}{z_t}\sum_{i=1}^t e^{\kappa_i}\eta_i\boldsymbol{v}_i}}\end{equation}
代入$\boldsymbol{m}_t,\boldsymbol{v}_t$的展开式得
\begin{gather}
\bar{\boldsymbol{m}}_t = \frac{1}{z_t}\sum_{i=1}^t e^{\kappa_i}\eta_i\boldsymbol{m}_i = \frac{1 - \beta_1}{z_t}\sum_{i=1}^t e^{\kappa_i}\eta_i\sum_{j=1}^i \beta_1^{i-j}\boldsymbol{g}_j = \sum_{j=1}^t\boldsymbol{g}_j\underbrace{\frac{1 - \beta_1}{z_t}\sum_{i=j}^t e^{\kappa_i}\beta_1^{i-j}\eta_i}_{\text{记为}\bar{\beta}_1(j,t)} \\
\bar{\boldsymbol{v}}_t = \frac{1}{z_t}\sum_{i=1}^t e^{\kappa_i}\eta_i\boldsymbol{v}_i = \frac{1 - \beta_2}{z_t}\sum_{i=1}^t e^{\kappa_i}\eta_i\sum_{j=1}^i \beta_2^{i-j}\boldsymbol{g}_j^2 = \sum_{j=1}^t\boldsymbol{g}_j^2\underbrace{\frac{1 - \beta_2}{z_t}\sum_{i=j}^t e^{\kappa_i}\beta_2^{i-j}\eta_i}_{\text{记为}\bar{\beta}_2(j,t)} \\
\end{gather}
可以看到，跟静态Weight Decay和Learning Rate相比，动态版形式上并没有太大变化，只不过梯度的加权系数变成了稍微复杂一点的$\bar{\beta}_1(j,t)$和$\bar{\beta}_2(j,t)$。特别地，当$\beta_1,\beta_2\to 0$时，$\bar{\beta}_1(j,t)$和$\bar{\beta}_2(j,t)$简化为
\begin{equation}\bar{\beta}_1(j,t) = \bar{\beta}_2(j,t) = \frac{e^{\kappa_j}\eta_j}{z_t}\label{eq:bb1-bb2-0}\end{equation}

最优调度 #

接下来可以做的事情有很多，最基本的就是根据具体的WD Schedule和LR Schedule去算$\bar{\beta}_1(j,t)$和$\bar{\beta}_2(j,t)$、估计记忆周期等。不过，这里我们选择做一件更极致的事情——直接去反推一个最优的WD Schedule和LR Schedule。

具体来说，前面我们假设了数据已经全局打乱，那么每个Batch的数据都同等重要，但静态版得到的系数$\bar{\beta}_1(j,t)\propto\beta_3^{t-j+1} - \beta_1^{t-j+1}$并非常数，而是随距离变化，这跟“每个Batch的数据都同等重要”不完全吻合。如果条件允许，那么我们期望它应该恒等于某个常数。根据这个期望，我们就可以反解出对应的$\lambda_j,\eta_j$。

简单起见，我们从$\beta_1,\beta_2\to 0$的特例入手，此时希望求解的方程是$e^{\kappa_j}\eta_j/z_t = c_t$，其中$c_t$是某个只依赖于$t$的函数。注意上面说的“常数”是对于$j$而言的，$t$是训练的终点，常数可以与它有关。为了简化求解，我们用积分代替求和，即$\kappa_s \approx \int_0^s \lambda_{\tau} \eta_{\tau} d\tau$，那么方程变为$\exp\left(\int_0^s \lambda_{\tau} \eta_{\tau} d\tau\right)\eta_s \approx c_t z_t$。两边取对数，然后对$s$求导得
\begin{equation}\lambda_s \eta_s + \frac{\dot{\eta}_s}{\eta_s} \approx 0 \label{eq:lr-wd-ode}\end{equation}
如果$\lambda_s$取常数$\lambda$，那么可以解得
\begin{equation}\eta_s \approx \frac{\eta_{\max}}{\lambda\eta_{\max} s + 1}\label{eq:opt-lrt-wd}\end{equation}
这便是常数Weight Decay下的最佳LR Schedule，它不需要预设终点$t$和最小学习率$\eta_{\min}$，这意味着它可以无限训练下去，类似于WSD的Stable阶段，但它能自动平衡每一步梯度的系数。不过它也有个缺点：$s\to\infty$时它会趋于0。从《AdamW的Weight RMS的渐近估计（下）》可知Weight RMS会趋于$\lim\limits_{s\to\infty} \frac{\eta_s}{2\lambda_s}$，所以该缺点可能带来权重坍缩的风险。

为了解决这个问题，我们可以考虑让$\lambda_s = \alpha\eta_s$，$\alpha=\lambda_{\max}/\eta_{\max}$是一个常数，此时可以解得
\begin{equation}\eta_s \approx \frac{\eta_{\max}}{\sqrt{2\lambda_{\max}\eta_{\max} s + 1}},\qquad \lambda_s \approx \frac{\lambda_{\max}}{\sqrt{2\lambda_{\max}\eta_{\max} s + 1}} \label{eq:opt-lrt-wdt}\end{equation}
相应的$e^{\kappa_s} \approx \sqrt{2\lambda_{\max}\eta_{\max} s + 1}, e^{\kappa_s}\eta_s \approx \eta_{\max}, z_t\approx \eta_{\max} t, \bar{\beta}_1(j,t) = \bar{\beta}_2(j,t) \approx 1/t$。

一般结果 #

目前的结果，比如式$\eqref{eq:opt-lrt-wd}$和式$\eqref{eq:opt-lrt-wdt}$，都是基于$\beta_1,\beta_2=0$的，当它们不等于0时，结果需要变化吗？更一般地，上述结果都是基于Adam优化器的，它们多大程度上可以推广到其他优化器呢？

首先来看$\beta_1,\beta_2\neq 0$时的问题，答案是当$t$足够大时，结论并不用大改。以$\bar{\beta}_1(j,t)$为例，在上述最优调度下$e^{\kappa_i}\eta_i$等于（跟$t$有关的）常数，那么根据定义
\begin{equation}\bar{\beta}_1(j,t) = \frac{1 - \beta_1}{z_t}\sum_{i=j}^t e^{\kappa_i}\beta_1^{i-j}\eta_i \propto \sum_{i=j}^t \beta_1^{i-j} = \frac{1 - \beta_1^{t-j+1}}{1 - \beta_1}\end{equation}
当$t$足够大时$\beta_1^{t-j+1}\to 0$，所以这也可以看成是一个跟$j$无关的常数。前面也说了，对于$\beta_1,\beta_2$来说，“$t$足够大”这件事情几乎时肯定的，所以直接用$\beta_1,\beta_2=0$的结果就行。

至于优化器，前面我们提到的优化器有SGDM、RMSProp、Adam、SignSGDM、Muon，它们可以分为两类。其中，SGDM是一类，它的$\bar{\boldsymbol{u}}_t$直接就是$\bar{\boldsymbol{m}}_t$，连平均场近似都不需要用，所以直到式$\eqref{eq:lr-wd-ode}$的结果都是适用的。不过，式$\eqref{eq:opt-lrt-wd}$和式$\eqref{eq:opt-lrt-wdt}$大概不是最适合的了，因为SGDM的渐近Weight RMS还依赖于梯度模长（参考），所以要把梯度模长考虑进去才行，相对复杂一些。

剩下的RMSProp、Adam、SignSGDM、Muon我们将它归为另一类，都属于自适应学习率优化器，它们的更新规则都具有$\frac{\text{梯度}}{\sqrt{\text{梯度}{}^2}}$的其次形式，这种情况下，如果我们依旧相信平均场近似，那么就能得到同样的$\bar{\boldsymbol{m}}_t$、同样的$\beta_1(j,t)$，所以到式$\eqref{eq:lr-wd-ode}$的结果也是适用的；并且对于这类齐次型优化器，可以证明Weight RMS同样渐近正比于$\sqrt{\eta/\lambda}$，所以连同式$\eqref{eq:opt-lrt-wd}$和式$\eqref{eq:opt-lrt-wdt}$也可以复用。

假设讨论 #

我们的推导暂告一段落，这一节我们来讨论一下推导所依赖的假设。

纵观全文，推导过程中所用到的值得拿出来讨论的大假设主要有两个。第一个假设是平均场近似，首次介绍于《重新思考学习率与Batch Size（二）：平均场》。平均场本身肯定不是新的，它是物理学中的经典近似，但将其用来分析优化器的相关动态，应该是笔者首次引入的，目前已经用它估算过优化器的Batch Size、Update RMS、Weight RMS等，结果看起来是合理的。

对于平均场近似的有效性，其实我们没法评述太多，它更多体现了一种信仰。一方面，我们根据已有的估算结果的合理性，相信它会继续合理下去，至少能对一些标量指标给出有效的渐近估计。另一方面，对于自适应学习率优化器，由于其更新规则的非线性，分析难度大大增加，除了平均场近似外，我们其实也没什么计算工具能用了。

这其中最典型的例子就是Muon，因为它是非Element-wise的运算，以往像SignSGD那样逐分量的计算手段便失去了作用，而平均场近似依然奏效（参考《重新思考学习率与Batch Size（三）：Muon》）。所以，平均场近似实际上为一大类自适应学习率优化器的分析和估计提供了统一、有效、简洁的计算手段，目前看来似乎没有别的方法有同样的效果，所以我们只能继续相信它。

第二个大的假设是“每一步梯度只包含当前Batch的信息”，这个假设本质上是错误的，因为梯度不仅依赖于当前Batch的数据，还依赖于上一步的参数，而上一步的参数自然是包含了历史信息。不过，我们可以尝试补救一下，因为理论上来说，每个Batch都会带来新的信息，否则这个Batch就没有存在的意义了，所以补救的方法是改为“每一步梯度包含大致相同的增量信息”。

当然，仔细思考之下这个说法也是有争议的，因为学得越多，覆盖面越广，后来Batch的独特信息就越少。不过，还可以挣扎一下，那就是将知识分为“规律”和“事实”两大类，事实型知识——比如某个定理是某个数学家发现的——只能靠记忆，那么可以考虑改为“每一步梯度包含大致相同的事实型知识”。总之，从实践来看，“平等对待每一步梯度”所得的LR Schedule似乎真的是有好处的，所以总可以尝试为它构造一个解释。

最近的论文《How Learning Rate Decay Wastes Your Best Data in Curriculum-Based LLM Pretraining》提供了一个间接证据。它考虑了数据质量从低到高的课程学习，发现激进的LR Decay会让课程学习优势全无。而我们的结果是每一Batch的权重是式$\eqref{eq:bb1-bb2-0}$，正比于Learning Rate，如果LR Decay过于激进，那么后面的高质量数据权重反而过小，因而效果欠佳。能够合理解释这个现象，反过来显示了我们假设的合理性。

文章小结 #

本文从滑动平均的视角来理解权重衰减（WD）和学习率（LR），并探讨了在该视角下最优的WD Schedule和LR Schedule。

转载到请包括本文地址：https://www.kexue.fm/archives/11459

更详细的转载事宜请参考：《科学空间FAQ》