生成扩散模型漫谈（二十三）：信噪比与大图生成（下）

上一篇文章《生成扩散模型漫谈（二十二）：信噪比与大图生成（上）》中，我们介绍了通过对齐低分辨率的信噪比来改进noise schedule，从而改善直接在像素空间训练的高分辨率图像生成（大图生成）的扩散模型效果。而这篇文章的主角同样是信噪比和大图生成，但做到了更加让人惊叹的事情——直接将训练好低分辨率图像的扩散模型用于高分辨率图像生成，不用额外的训练，并且效果和推理成本都媲美直接训练的大图模型！

这个工作出自最近的论文《Upsample Guidance: Scale Up Diffusion Models without Training》，它巧妙地将低分辨率模型上采样作为引导信号，并结合了CNN对纹理细节的平移不变性，成功实现了免训练高分辨率图像生成。

思想探讨 #

我们知道，扩散模型的训练目标是去噪（Denoise，也是DDPM的第一个D）。按我们的直觉，去噪这个任务应该是分辨率无关的，换句话说，理想情况下低分辨率图像训练的去噪模型应该也能用于高分辨率图像去噪，从而低分辨率的扩散模型应该也能直接用于高分辨率图像生成。

有这么理想吗？笔者用之前自己训练的128*128的人脸图像（CelebA-HQ）扩散模型试了一下，即直接将它当成256*256的模型来推理，生成结果的画风是这样的：

将128分辨率的扩散模型当256分辨率用的生成效果

可以看到，生成结果有两个特点：

1、生成结果已经完全不是人脸图，说明128*128训练的去噪模型无法直接当成256*256的来用；

2、生成结果虽然不理想，但很清晰，没有明显模糊或者棋盘效应，且保留了一些人脸的纹理细节。

我们知道，直接将小图放大（上采样），就是一个最最基本的大图生成模型，但取决于上采样算法的不同，直接放大后的图片通常都会有模糊或者棋盘效应的出现，即缺乏足够的纹理细节。这时候一个“异想天开”的想法是：既然小图放大缺乏细节，而直接将小图模型当大图模型推理会保留一些细节，那么我们可否用后者给前者补充细节？

这就是原论文所提方法的核心思想。

数学描述 #

这一节我们用公式把思路重新整理一下，看下一步该怎么做。

首先统一一下符号。我们目标图像分辨率是$w\times h$，训练图像分辨率是$w/s\times h/s$，所以下面的$\boldsymbol{x},\boldsymbol{\varepsilon}$都是$w\times h\times 3$大小（对于图像来说还有个通道维度），而$\boldsymbol{x}^{\text{low}},\boldsymbol{\varepsilon}^{\text{low}}$都是$w\times h\times 3$大小，$\mathcal{D}$是将$w\times h$分辨率平均Pooling到$w/s\times h/s$的下采样算子，$\mathcal{U}$则是将$w/s\times h/s$分辨率最邻近插值（即直接重复）到$w\times h$的上采样算子。

我们知道，扩散模型需要一个训练好的去噪模型$\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)$，以DDPM为例（这里采用的是《生成扩散模型漫谈（三）：DDPM = 贝叶斯 + 去噪》一文的形式，跟主流形式基本对齐），它的推理格式为
\begin{equation}\boldsymbol{x}_{t-1} = \frac{1}{\alpha_t}\left(\boldsymbol{x}_t - \frac{\beta_t^2}{\bar{\beta}_t}\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\right) + \sigma_t \boldsymbol{\varepsilon},\quad \boldsymbol{\varepsilon}\sim\mathcal{N}(\boldsymbol{0}, \boldsymbol{I})\end{equation}
其中$\sigma_t$的主流取法是$\frac{\bar{\beta}_{t-1}\beta_t}{\bar{\beta}_t}$或者$\beta_t$。但现在我们没有在$w\times h$分辨率下训练好的$\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)$，只有一个$w/s\times h/s$分辨率下训练好的$\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t^{\text{low}}, t)$。

根据我们的经验，将大图缩小后再放大，虽然会导致失真，但它还可以算是原图的一个比较好的近似。这启发我们，去噪模型可以类似地构建出一个主项出来，具体来说，为了对$w\times h$大小的图像去噪，我们可以先将它缩小（下采样，平均Pooling）到$w/s\times h/s$，然后送入在$w/s\times h/s$分辨率训练好的去噪模型中进行去噪，最后将去噪结果放大（上采样）到$w\times h$，这样虽然不是理想的去噪结果，但应该已经是理想结果的一个主项。

接着，上一节我们演示了直接将低分辨率训练的去噪模型当成高分辨率模型用，能够保留一些纹理细节，所以我们可以认为完全不加改动的$\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)$则可以构成一个描绘细节的次要项。想办法将这主、次两项整合在一起，也许我们就可以得到精准去噪模型的一个足够好的近似，从而实现免训练的高分辨率扩散生成。

再请SNR #

现在我们来讨论主项。首先我们明确，这篇文章并不是要重新训练一个高分辨率模型，而是要复用原本的低分辨率模型到高分辨率输入上，所以noise schedule还是原来的$\bar{\alpha}_t,\bar{\beta}_t$，于是我们可以假定同样有
\begin{equation}\boldsymbol{x}_t = \bar{\alpha}_t \boldsymbol{x}_0 + \bar{\beta}_t \boldsymbol{\varepsilon}\end{equation}
其中$\boldsymbol{\varepsilon}$是标准正态分布的向量。根据上一节所述，主项需要先下采样后再去噪，设$\mathcal{D}$代表下采样到$w/s\times h/s$的平均Pooling运算，那么我们有
\begin{equation}\mathcal{D}[\boldsymbol{x}_t] = \bar{\alpha}_t \mathcal{D}[\boldsymbol{x}_0] + \frac{\bar{\beta}_t}{s} \boldsymbol{\varepsilon}\label{eq:dx}\end{equation}
这里的相等指的是服从同一分布。在上一篇文章中，我们引入了信噪比$SNR(t)=\frac{\bar{\alpha}_t^2}{\bar{\beta}_t^2}$，由此可见$\boldsymbol{x}_t$的信噪比是$\frac{\bar{\alpha}_t^2}{\bar{\beta}_t^2}$，但$\mathcal{D}[\boldsymbol{x}_t]$的信噪比是$\frac{s^2\bar{\alpha}_t^2}{\bar{\beta}_t^2}$。根据本文的设置，去噪模型$\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)$只在noise schedule为$\bar{\alpha}_t,\bar{\beta}_t$的低分辨率图像上训练过，这意味着$t$时刻的$\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)$适用的输入信噪比是$\frac{\bar{\alpha}_t^2}{\bar{\beta}_t^2}$，但$\mathcal{D}[\boldsymbol{x}_t]$的信噪比是$\frac{s^2\bar{\alpha}_t^2}{\bar{\beta}_t^2}$，所以直接用$t$时刻的模型效果不是最佳的。

那怎么办呢？很简单，信噪比随着时间$t$的变化而变化，我们可以找另一个时刻$\tau$，使得它的信噪比就是$\frac{s^2\bar{\alpha}_t^2}{\bar{\beta}_t^2}$，也就是解方程
\begin{equation}\frac{\bar{\alpha}_{\tau}^2}{\bar{\beta}_{\tau}^2} = \frac{s^2\bar{\alpha}_t^2}{\bar{\beta}_t^2}\end{equation}
解出$\tau$后，我们就得到$\tau$时刻的模型更适合于信噪比为$\frac{s^2\bar{\alpha}_t^2}{\bar{\beta}_t^2}$的输入，于是$\mathcal{D}[\boldsymbol{x}_t]$的去噪应该适用$\tau$时刻而不是$t$时刻的模型。此外，$\mathcal{D}[\boldsymbol{x}_t]$本身还可以改进一下，从式$\eqref{eq:dx}$可以发现当$s > 1$时两个系数平方和$\rho_t^2=\bar{\alpha}_t^2+\frac{\bar{\beta}_t^2}{s^2}$不再是1，而训练阶段的系数平方和都是1，所以我们可以将它除以$\rho_t$，使其更接近训练结果的形式。最终由$\mathcal{D}[\boldsymbol{x}_t]$构建的去噪模型主项应该是
\begin{equation}\boldsymbol{\epsilon}_{\boldsymbol{\theta}}\left(\frac{\mathcal{D}[\boldsymbol{x}_t]}{\rho_t}, \tau\right)\label{eq:down-denoise}\end{equation}

分解近似 #

现在有两个去噪模型可以用，一项是直接将低分辨率模型$\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t^{\text{low}}, t)$当高分辨率用的$\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)$，另一项是上一节推出来的先下采样再去噪的模型$\eqref{eq:down-denoise}$，接下来我们就可以尝试将它们组装起来了。

假设我们有一个经过高分辨率图像训练过的完美去噪模型$\boldsymbol{\epsilon}^{\text{high}}(\boldsymbol{x}_t, t)$，那么我们可以将它分解为
\begin{equation}\boldsymbol{\epsilon}^{\text{high}}(\boldsymbol{x}_t, t) = \underbrace{\color{red}{\mathcal{U}\left[\mathcal{D}\left[\boldsymbol{\epsilon}^{\text{high}}(\boldsymbol{x}_t, t)\right]\right]}}_{\text{低分辨率主项}} + \underbrace{\Big\{\color{green}{\boldsymbol{\epsilon}^{\text{high}}(\boldsymbol{x}_t, t) - \mathcal{U}\left[\mathcal{D}\left[\boldsymbol{\epsilon}^{\text{high}}(\boldsymbol{x}_t, t)\right]\right]}\Big\}}_{\text{高分辨率细节项}}\end{equation}
咋看上去，这个分解只是简单的恒等变换，但实际上它有非常直观的意义：第一项是将精确的重构结果先下采样然后上采样，说白了先缩小后放大，这是一个有损变换，但得到的结果还是足以描绘主体轮廓，所以它是主项；第二项则是将精确结果减去主体轮廓，得到的很明显就代表着局部细节。

结合我们之前讨论的思路，我们认为上一节所给出的式$\eqref{eq:down-denoise}$是低分辨率主项的一个良好近似，所以我们写出
\begin{equation}\mathcal{D}\left[\boldsymbol{\epsilon}^{\text{high}}(\boldsymbol{x}_t, t)\right]\approx \frac{1}{s}\boldsymbol{\epsilon}_{\boldsymbol{\theta}}\left(\frac{\mathcal{D}[\boldsymbol{x}_t]}{\rho_t}, \tau\right)\end{equation}
注意不能漏了前面的因子$1/s$，这是因为去噪模型通常预测的是标准正态噪声（即$\boldsymbol{\varepsilon}$），因此它的输出本身近似满足零均值和单位方差，经过下采样$\mathcal{D}$之后方差变为$1/s^2$，而$\boldsymbol{\epsilon}_{\boldsymbol{\theta}}$的输出同样是单位方差的，所以要除以$s$使得方差变为$1/s^2$，以提高近似程度。

对于高分辨率细节项，我们则写出：
\begin{equation}\boldsymbol{\epsilon}^{\text{high}}(\boldsymbol{x}_t, t) - \mathcal{U}\left[\mathcal{D}\left[\boldsymbol{\epsilon}^{\text{high}}(\boldsymbol{x}_t, t)\right]\right]\approx \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t) - \mathcal{U}\left[\mathcal{D}\left[\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\right]\right]\end{equation}
这同样是基于前面讨论的思路——直接将低分辨率去噪模型当高分辨率模型用，其中纹理细节的地方保留得比较好，所以我们认为对于高分辨率细节，$\boldsymbol{\epsilon}_{\boldsymbol{\theta}}$就是$\boldsymbol{\epsilon}^{\text{high}}$的一个良好近似。

综合这两项近似，我们就可以完整地写出：
\begin{equation}\boldsymbol{\epsilon}^{\text{high}}(\boldsymbol{x}_t, t)\approx \frac{1}{s}\mathcal{U}\left[\boldsymbol{\epsilon}_{\boldsymbol{\theta}}\left(\frac{\mathcal{D}[\boldsymbol{x}_t]}{\rho_t}, \tau\right) \right]+ \Big\{\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t) - \mathcal{U}\left[\mathcal{D}\left[\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\right]\right]\Big\}\triangleq \boldsymbol{\epsilon}_{\boldsymbol{\theta}}^{\text{approx}}(\boldsymbol{x}_t, t)\label{eq:high-key}\end{equation}
这就是我们要寻找的高分辨率去噪模型的关键近似！

事实上，直接用式$\eqref{eq:high-key}$来生成高分辨率图已经有不错的效果了，但我们还可以引入一个可调的超参数，使其可以做得更好一些。具体思路是模仿《生成扩散模型漫谈（九）：条件控制生成结果》通过无条件模型来加强条件生成的做法，我们将$\boldsymbol{\epsilon}_{\boldsymbol{\theta}}^{\text{approx}}(\boldsymbol{x}_t, t)$看成是条件去噪模型，其中引导信号就是低分辨率上采样的主项（即论文标题的“Upsample Guidance”，简称UG），而$\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)$则看成是无条件去噪模型，我们要加强条件，所以引入可调参数$w > 0$，将最终所用的去噪模型表示为
\begin{equation}\begin{aligned}
\tilde{\boldsymbol{\epsilon}}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t) =&\, (1 + w)\, \boldsymbol{\epsilon}_{\boldsymbol{\theta}}^{\text{approx}}(\boldsymbol{x}_t, t) - w\,\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t) \\
=&\, \boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t) + (1 + w)\mathcal{U}\left[\frac{1}{s}\boldsymbol{\epsilon}_{\boldsymbol{\theta}}\left(\frac{\mathcal{D}[\boldsymbol{x}_t]}{\rho_t}, \tau\right) - \mathcal{D}\left[\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)\right]\right]
\end{aligned}\end{equation}
根据原论文的实验结果，$w=0.2$附近的效果比较好。

LDM扩展 #

虽然在形式上前述结果似乎不区分是Pixel空间的扩散模型还是隐空间的扩散模型（LDM），但事实上从理论的角度看前述结果只适用于Pixel空间的扩散模型，LDM多了一个非线性的Encoder，大图经过Encoder之后的特征，Pooling之后未必等于小图经过Encoder之后的特征，因此我们通过先下采样后上采样来近似构建高分辨率去噪模型的主项这一假设未必还成立。

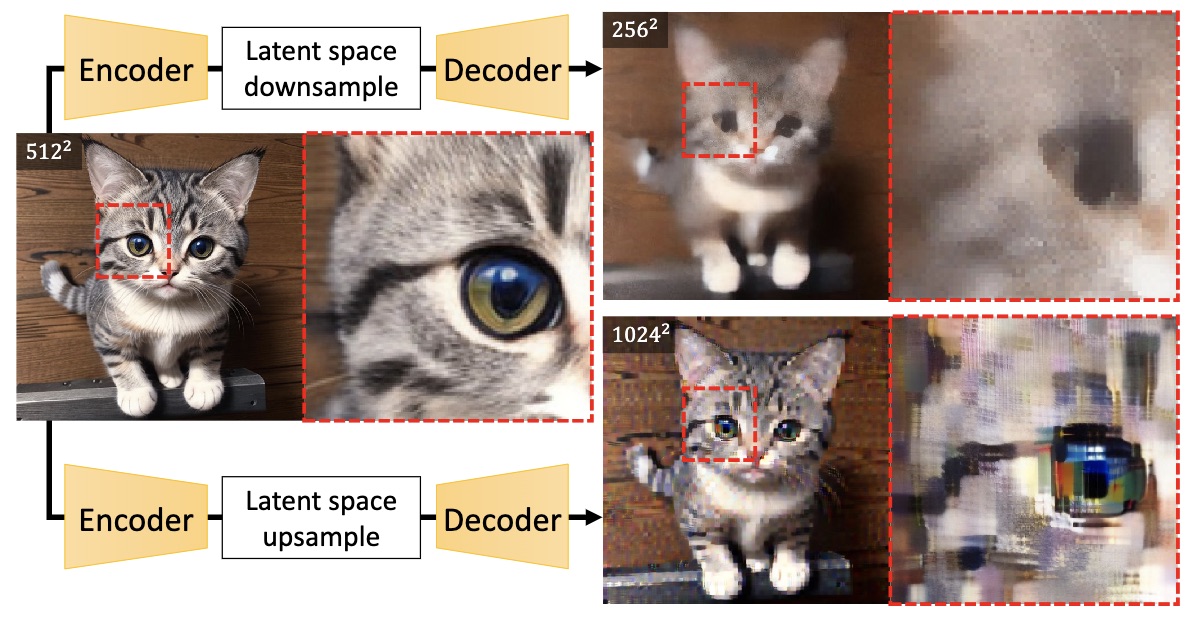
为了观察LDM场景下有什么不同之处，我们可以看原论文的两个实验结果。第一个是将Encoder的特征上/下采样后送入Decoder后的重建结果，如下图所示。结果显示不管是上采样还是下采样，直接在特征空间进行此类操作，都会导致图像的劣化，这意味着先通过下采样去噪然后上采样构建的主项权重或许要适当降低。

对Encoder的特征进行上:下采样，都会导致Decoder的结果劣化

第二个实验是直接将低分辨率的LDM不加改动地当高分辨率模型用，其结果送入Decoder后的生成结果可以参考下图的“w/o UG”部分。可以看到，跟Pixel空间的扩散模型不同，大体是得益于Decoder对特征的鲁棒性，LDM场景下$\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)$直接当高分辨率模型用的效果理想很多，语义和清晰度都有明显保证，只是个别地方出现了一些“畸形”。

是否加Upsample Guidance（UG）的小图LDM用于生成大图的效果区别

基于这两个实验结论，原论文将LDM场景下的$w$改为跟时间$t$相关的函数：
\begin{equation}w_t = \left\{\begin{aligned}
w,\quad t \geq (1-\eta) T \\
-1,\quad t < (1-\eta) T
\end{aligned}\right.\end{equation}
当$w = -1$时，Upsample Guidance就等价于不存在，这就相当于说Upsample Guidance只加在扩散前期，这既能够在前期通过Upsample Guidance更好地防止畸形，又能够在后期充分利用$\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)$生成更清晰锐利的结果，同时还节省计算量，可谓“一箭三雕”了。

效果演示 #

终于来到实验环节了。其实上一节的图片中的“w/ UG”部分，已经演示了Upsample Guidance在LDM场景的效果，可以看到Upsample Guidance确实能纠正$\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)$直接用于高分辨率生成带来的畸形，同时保证语义的正确性和图像的清晰度。

至于Pixel空间的生成效果，则可以参考下图：

原论文演示的Upsample Guidance在Pixel扩散模型上的效果

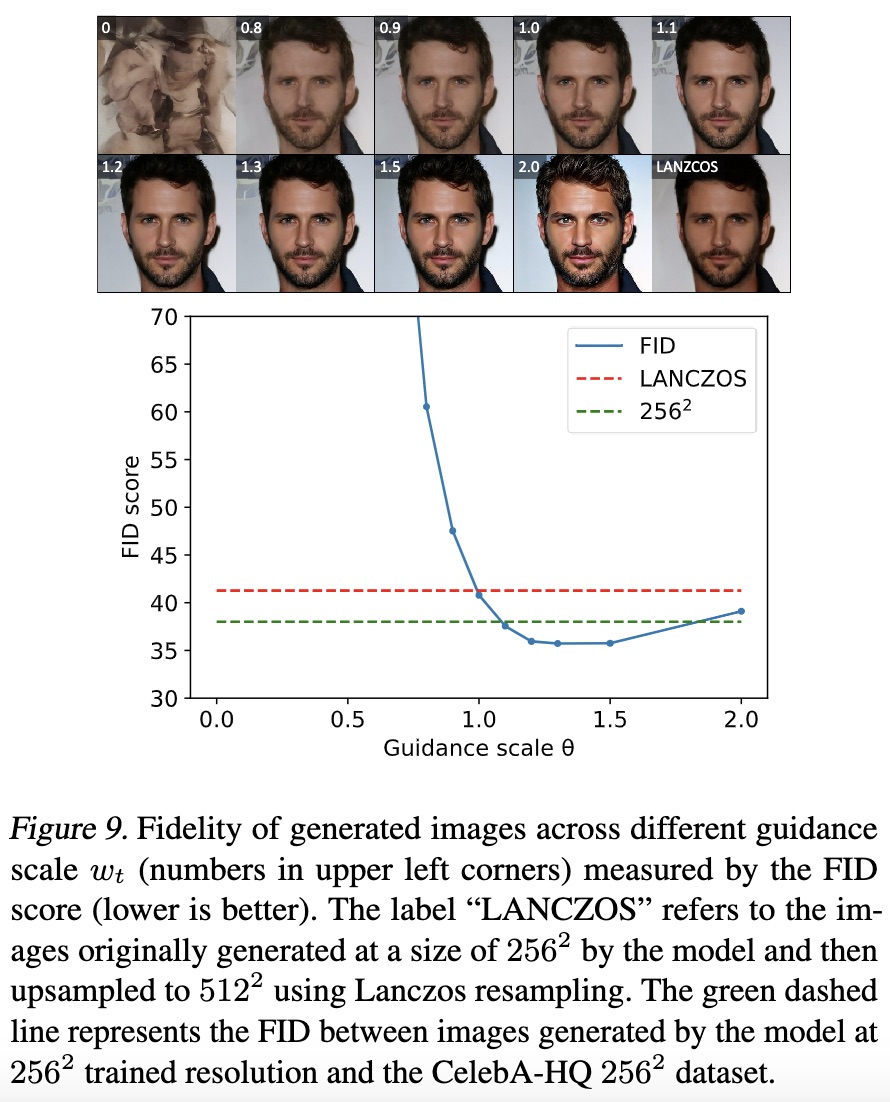
由于Upsample Guidance的存在，整个方法有点像是先生成低分辨率图像然后通过超分辨率方法生成高清图，只不过它是以无监督的方法进行，所以基本上可以保证FID等不差于低分辨率的生成结果：

FID指标与超参数关系（它这里的wt和θ等于本文的w加上1）

最后，笔者也用自己之前训练的128*128的CelebA人脸扩散模型进行了尝试，进一步肯定了Upsample Guidance的有效性：

个人实验效果。左边是训练分辨率（128）生成效果，中、右分别是Upsample Guidance生成的256、512分辨率生成效果

效果上，肯定不如直接训练的高分辨率模型，但比低分辨率图直接放大效果要好；推理成本上，相比于将$\boldsymbol{\epsilon}_{\boldsymbol{\theta}}(\boldsymbol{x}_t, t)$用高分辨率图像训练后直接用于生成，Upsample Guidance多了一项低分辨率的计算，计算成本的增加比例大致上是$1/s^2$，如果是LDM则由于生成后期不加入Upsample Guidance，因此这个比例还更少。总的来说，Upsample Guidance称得上是成本合理的大图生成免费午餐了。

思考分析 #

看完Upsample Guidance整个框架，不知道大家的感受是什么？笔者的感觉是非常像物理学家的风格，天马行空、大胆假设但又在无形之中把握住了本质。这类工作让笔者写个解读或许没啥问题，但自己独立想出来的话是万万不可能的，因为笔者充其量也只有一点很死板的数学思维。

关于Upsample Guidance的一个很自然的疑问是：它有效的原因究竟是什么？以笔者在Pixel空间训练的CelelbA人脸生成模型为例，它只在128*128的小图上训练过，完全没见过256*256的大图，那它为什么能恰如其分地生成符合我们认知的256*256大图？注意这还跟ImageNet不同，ImageNet数据集是一个多尺度的数据集，比如一张128*128的图，它可能是一条鱼，也可以是一个人手里拿着一条鱼，也就是说虽然都是128*128的输入，但它见过不同比例的鱼，从而能更好地适应不同的分辨率，但CelelbA不一样，它是单尺度的数据集，所有人脸的大小、位置、朝向都是对齐的，但即便如此，Upsample Guidance依然可以成功地将它泛化到了

笔者认为，这多少跟DIP（Deep Image Prior）有点联系。DIP的大致意思是说，CV常用的CNN模型，其架构本身就已经经过高度筛选，非常契合视觉本身，所以哪怕不经过真实数据训练的模型，也能够完成一些视觉任务，如去噪、补全甚至简单的超分等。Upsample Guidance可以让完全没见过大图的扩散模型生成基本合乎认知的大图，看上去也是得益于CNN本身的架构先验。简单来讲，正如本文第一节所实验的，Upsample Guidance依赖于直接将低分辨率模型当高分辨率模型用，生成结果至少保留了一些有效的纹理细节，这一点并不是平凡的性质。

为了验证这一点，笔者特意去拿之前训练的纯Transformer扩散模型（有点类似DiT + RoPE-2D）去尝试了一下，发现完全不能重现Upsample Guidance的效果，这表明它至少是对CNN-based的U-Net模型架构有所依赖的。不过用Transformer的读者也不用灰心，它虽然不能走Upsample Guidance的路线，但可以走NLP的长度外推的路线。《FiT: Flexible Vision Transformer for Diffusion Model》一文表明，通过Transformer + RoPE-2D的组合训练扩散模型，可以复用NTK、YaRN等长度外推技术，达到免训练或者极少量的微调就可以生成高分辨率图的效果。

文章小结 #

这篇文章介绍了一个名为Upsample Guidance的技巧，它可以让训练好的低分辨率扩散模型直接生成高分辨率图片，而不需要额外的微调成本，实验显示它基本上能稳定提高至少1倍的分辨率，虽然效果离直接训练的高分辨率扩散模型还有点差距，但这近乎免费的午餐依然值得学习一番。本文从笔者的角度重新整理了该方法的思路和推导，并给出了关于其有效性原因的思考。

（后记：事实上，按照最初的计划，这篇文章是在两天前发布的，之所以推迟了两天，是因为在写作过程中笔者发现很多开始自以为理解的细节，实际上还含糊不清，所以多花了两天时间进行推导和实验，以获得更精准的理解。由此可见，将要学习的东西系统清晰地重述出来，本身也是一个不断自我完善和改进的过程，这大概就是坚持写作的意义所在吧。）

转载到请包括本文地址：https://kexue.fm/archives/10055

更详细的转载事宜请参考：《科学空间FAQ》

打赏

微信打赏

支付宝打赏

因为网站后台对打赏并无记录，因此欢迎在打赏时候备注留言。
你还可以点击这里或在下方评论区留言来告知你的建议或需求。