从动力学角度看优化算法（一）：从SGD到动量加速

在这个系列中，我们来关心优化算法，而本文的主题则是SGD（stochastic gradient descent，随机梯度下降），包括带Momentum和Nesterov版本的。对于SGD，我们通常会关心的几个问题是：

SGD为什么有效？
SGD的batch size是不是越大越好？
SGD的学习率怎么调？
Momentum是怎么加速的？
Nesterov为什么又比Momentum稍好？
...

这里试图从动力学角度分析SGD，给出上述问题的一些启发性理解。

梯度下降 #

既然要比较谁好谁差，就需要知道最好是什么样的，也就是说我们的终极目标是什么？

训练目标分析 #

假设全部训练样本的集合为$\boldsymbol{S}$，损失度量为$L(\boldsymbol{x};\boldsymbol{\theta})$，其中$\boldsymbol{x}$代表单个样本，而$\boldsymbol{\theta}$则是优化参数，那么我们可以构建损失函数
$$L(\boldsymbol{\theta}) = \frac{1}{|\boldsymbol{S}|}\sum_{\boldsymbol{x}\in\boldsymbol{S}} L(\boldsymbol{x};\boldsymbol{\theta})\tag{1}$$
而训练的终极目标，则是找到$L(\boldsymbol{\theta})$的一个全局最优点（这里的最优是“最小”的意思）。

GD与ODE #

为了完成这个目标，我们可以用梯度下降法（gradient descent，GD）：
$$\boldsymbol{\theta}_{n+1}=\boldsymbol{\theta}_{n} - \gamma \nabla_{\boldsymbol{\theta}} L(\boldsymbol{\theta}_{n})\tag{2}$$
其中$\gamma > 0$称为学习率，这里刚好也是迭代的步长（后面我们会看到步长不一定等于学习率）。梯度下降有多种理解方式，由于一般都有$\gamma \ll 1$，所以这里我们将它改变为
$$\frac{\boldsymbol{\theta}_{n+1}-\boldsymbol{\theta}_{n}}{\gamma} = - \nabla_{\boldsymbol{\theta}} L(\boldsymbol{\theta}_{n})\tag{3}$$
那么左边就近似于$\boldsymbol{\theta}$的导数（假设它是时间$t$的函数），于是我们可以得到ODE动力系统：
$$\dot{\boldsymbol{\theta}} = - \nabla_{\boldsymbol{\theta}} L(\boldsymbol{\theta})\tag{4}$$
而$(2)$则是$(4)$的一个欧拉解法。这样一来，梯度下降实际上就是用欧拉解法去求解动力系统$(4)$，由于$(4)$是一个保守动力系统，因此它最终可以收敛到一个不动点（让$\dot{\boldsymbol{\theta}}=0$），并且可以证明稳定的不动点是一个极小值点（但未必是全局最小的）。

随机梯度下降 #

这里表明，随机梯度下降可以用一个随机微分方程来半定性、半定量地分析。

从GD到SGD #

$(2)$我们一般称为“全量梯度下降”，因为它需要所有样本来计算梯度，这是梯度下降的一个显著缺点：当样本成千上万时，每迭代一次需要的成本太大，甚至可能达到难以进行。于是我们想随机从$\boldsymbol{S}$中随机抽取一个子集$\boldsymbol{R}\subseteq \boldsymbol{S}$，然后只用$\boldsymbol{R}$去计算梯度并完成单次迭代。我们记
$$L_{\boldsymbol{R}}(\boldsymbol{\theta}) = \frac{1}{|\boldsymbol{R}|}\sum_{\boldsymbol{x}\in\boldsymbol{R}} L(\boldsymbol{x};\boldsymbol{\theta})\tag{5}$$
然后公式$(2)$变为
$$\boldsymbol{\theta}_{n+1}=\boldsymbol{\theta}_{n} - \gamma \nabla_{\boldsymbol{\theta}} L_{\boldsymbol{R}}(\boldsymbol{\theta}_{n})\tag{6}$$
注意$L$的最小值才是我们的目标，而$L_{\boldsymbol{R}}$则是一个随机变量，$\nabla_{\boldsymbol{\theta}} L_{\boldsymbol{R}}(\boldsymbol{\theta}_{n})$只是原来$\nabla_{\boldsymbol{\theta}} L(\boldsymbol{\theta}_{n})$的一个估计。这样做能不能得到合理的结果呢？

从SGD到SDE #

这里我们假设
$$\nabla_{\boldsymbol{\theta}} L(\boldsymbol{\theta}_{n}) - \nabla_{\boldsymbol{\theta}} L_{\boldsymbol{R}}(\boldsymbol{\theta}_{n})=\boldsymbol{\xi}_n\tag{7}$$
服从一个方差为$\sigma^2$的正态分布，注意这只是一个近似描述，主要是为了半定性、半定量分析。经过这样假设，随机梯度下降相当于在动力系统$(4)$中引入了高斯噪声：
$$\dot{\boldsymbol{\theta}} = - \nabla_{\boldsymbol{\theta}} L(\boldsymbol{\theta}) + \sigma \boldsymbol{\xi}\tag{8}$$
其中$\boldsymbol{\xi}$服从标准正态分布。原来的动力系统是一个ODE，现在变成了SDE（随机微分方程），我们称之为“朗之万方程”。当然，其实噪声的来源不仅仅是随机子集带来的估算误差，每次迭代的学习率大小也会带来噪声。

在噪声的高斯假设下，这个方程的解是怎样的呢？原来的ODE的解是一条确定的轨线，现在由于引入了一个随机噪声，因此解也是随机的，可以解得平衡状态的概率分布为
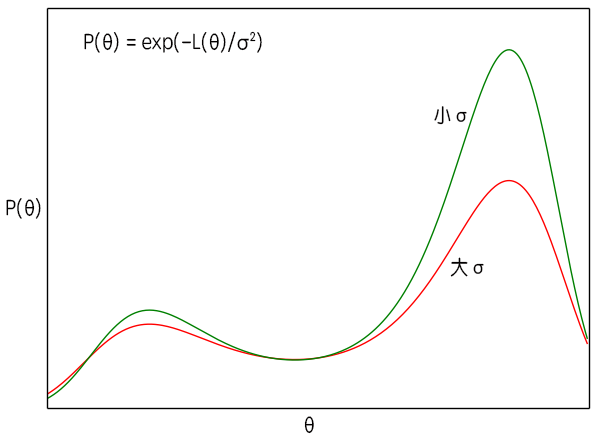
$$P(\boldsymbol{\theta}) \sim \exp \left(-\frac{L(\boldsymbol{\theta})}{\sigma^2}\right)\tag{9}$$
求解过程可以参考一般的随机动力学教程，我们只用到这个结果就好。

结果启发 #

从$(8)$式中我们可以得到一些有意义的结果。首先我们看到，原则上来说这时候的$\boldsymbol{\theta}$已经不是一个确定值，而是一个概率分布，而且原来$L(\boldsymbol{\theta})$的极小值点，刚好现在变成了$P(\boldsymbol{\theta})$的极大值点。这说明如果我们无限长地执行梯度下降的话，理论上$\boldsymbol{\theta}$能走遍所有可能的值，并且在$L(\boldsymbol{\theta})$的各个“坑”中的概率更高。

$\sigma^2$是梯度的方差，显然这个方差是取决于batch size的，根据定义$(7)$，batch size越大方差越小。而在$(9)$式中，$\sigma^2$越大，说明$P(\boldsymbol{\theta})$的图像越平缓，即越接近均匀分布，这时候$\boldsymbol{\theta}$可能就到处跑；当$\sigma^2$越小时，原来$L(\boldsymbol{\theta})$的极小值点的区域就越突出，这时候$\boldsymbol{\theta}$就可能掉进某个“坑”里不出来了。

这样分析的话，理论上来说，我们一开始要让batch size小一些，那么噪声方差$\sigma^2$就会大一些，越接近均匀分布，算法就会遍历更多的区域，随着迭代次数的增加，慢慢地就会越来越接近最优区域，这时候方差应该要下降，使得极值点更为突出。也就是说，有可能的话，batch size应该要随着迭代次数而缓慢增加。这就部分地解释了去年Google提出来的结果《学界 | 取代学习率衰减的新方法：谷歌大脑提出增加Batch Size》，不过batch size增加会大幅度增加计算成本，所以我们一般增加到一定量也就不去调整了。

当然，从图中可以看到，当进入稳定下降区域时，每次迭代的步长$\gamma$（学习率）就不应该超过“坑”的宽度，而$\sigma^2$越小，坑也就越窄，这也表明学习率应该要随着迭代次数的增加而降低。另外$\gamma$越大也部分地带来噪声，因此$\sigma^2$降低事实上也就意味着我们要降低学习率。

所以分析结果就是：

条件允许情况下，在使用SGD时，开始使用小batch size和大学习率，然后让batch size慢慢增加，学习率慢慢减小。

至于增大、减少的策略，就要靠各位的炼丹水平了。

动量加速 #

众所周知，相比Adam等自适应学习率算法，纯SGD优化是很慢的，而引入动量可以加速SGD的迭代。它也有一个漂亮的动力学解释。

从一阶到二阶 #

从前面的文字我们知道，SGD和GD在迭代格式上没有什么差别，所以要寻求SGD的加速，我们只需要寻求GD的加速，然后将全量梯度换成随机梯度就行了。而$(2)$式到$(4)$式的过程我们可以知道，GD将求$L(\boldsymbol{\theta})$的最小值问题变成了ODE方程$\dot{\boldsymbol{\theta}} = - \nabla_{\boldsymbol{\theta}} L(\boldsymbol{\theta})$的迭代求解问题。

那么，为什么一定要是一阶的呢？二阶的$\ddot{\boldsymbol{\theta}} = - \nabla_{\boldsymbol{\theta}} L(\boldsymbol{\theta})$行不？

为此，我们考虑一般的
$$\ddot{\boldsymbol{\theta}} + \lambda \dot{\boldsymbol{\theta}} = - \nabla_{\boldsymbol{\theta}} L(\boldsymbol{\theta})\tag{10}$$
这样就真正地对应一个（牛顿）力学系统了，其中$\lambda > 0$引入了类似摩擦力的作用。我们来分析这样的系统跟原来GD的一阶ODE$(4)$与$(10)$有什么差别。

首先，从不动点的角度看，$(10)$最终收敛到的稳定不动点（让$\ddot{\boldsymbol{\theta}}=\dot{\boldsymbol{\theta}}=0$），确实也是$L(\boldsymbol{\theta})$的一个极小值点。试想一下，一个小球从山顶滚下来，会自动掉到山谷又爬升，但是由于摩擦阻力的存在，最终就停留在山谷了。注意，除非算法停不了，否则一旦算法停了，那么一定是一个山谷（也有可能是山顶、鞍点，但从概率上来讲则是比较小的），但绝对不可能是半山腰，因为半山腰的话，还存在势能，由能量守恒定律，它可以转化为动能，所以不会停下来。

因此收敛情况跟一阶的GD应该是没有差别的，所以只要比较它们俩的收敛速度。

GD+Momentum #

我们将$(10)$等价地改写为
$$\dot{\boldsymbol{\theta}}=\boldsymbol{\eta},\quad \dot{\boldsymbol{\eta}}=-\lambda \boldsymbol{\eta} - \nabla_{\boldsymbol{\theta}} L(\boldsymbol{\theta})\tag{11}$$

我们将$\dot{\boldsymbol{\theta}}$离散化为
$$\dot{\boldsymbol{\theta}}\approx \frac{\boldsymbol{\theta}_{n+1}-\boldsymbol{\theta}_{n}}{\gamma}\tag{12}$$
那么$\boldsymbol{\eta}$要怎么处理呢？$\boldsymbol{\eta}_n$？不对不对，$(\boldsymbol{\theta}_{n+1}-\boldsymbol{\theta}_{n})/\gamma$作为$n$时刻的导数只有一阶近似（$\mathcal{O}(\gamma)$），而作为$n+1/2$时刻的导数则有二阶近似（$\mathcal{O}(\gamma^2)$）。所以，更准确地有：
$$\frac{\boldsymbol{\theta}_{n+1}-\boldsymbol{\theta}_{n}}{\gamma}=\boldsymbol{\eta}_{n+1/2}\tag{13}$$
类似地，从$(11)$式的第二个式子，我们导出下面的结果，同样具有二阶近似
$$\frac{\boldsymbol{\eta}_{n+1/2}-\boldsymbol{\eta}_{n-1/2}}{\gamma}=-\lambda\left(\frac{\boldsymbol{\eta}_{n+1/2}+\boldsymbol{\eta}_{n-1/2}}{2}\right)- \nabla_{\boldsymbol{\theta}} L(\boldsymbol{\theta}_n)\tag{14}$$
总而言之，为了追求高精度，$(\boldsymbol{\theta}_{n+1}-\boldsymbol{\theta}_{n})/\gamma$是$\boldsymbol{\theta}$的$n+1/2$时刻的导数，$(\boldsymbol{\eta}_{n+1/2}-\boldsymbol{\eta}_{n-1/2})/\gamma$是$\boldsymbol{\eta}$的$n$时刻的导数，而$(\boldsymbol{\eta}_{n+1/2}+\boldsymbol{\eta}_{n-1/2})/2=\boldsymbol{\eta}_n$。它们都具有$\mathcal{O}(\gamma^2)$的精度。
记
$$\boldsymbol{v}_{n+1}=\gamma\boldsymbol{\eta}_{n+1/2},\quad \beta = \frac{1-\lambda\gamma/2}{1+\lambda\gamma/2},\quad \alpha = \frac{\gamma^2}{1+\lambda\gamma/2}\tag{15}$$
那么联合$(13),(14)$我们得到
$$\begin{aligned}&\boldsymbol{\theta}_{n+1} = \boldsymbol{\theta}_{n} + \boldsymbol{v}_{n+1} \\ & \boldsymbol{v}_{n+1} = \beta\boldsymbol{v}_{n} - \alpha \nabla_{\boldsymbol{\theta}} L(\boldsymbol{\theta}_n) \end{aligned}\tag{16}$$
这就是带Momentum的GD算法了。在数学上，他还有一个特别的名字，叫做“蛙跳积分法”。

如何加速？ #

结合$(15)$和$(16)$两个式子，我们就可以观察到Momentum是如何加速GD了。

在GD的$(2)$中，学习率是$\gamma$，步长也是$\gamma$，精度是$\mathcal{O}(\gamma)$；在Momentum中，学习率是$\alpha\approx \gamma^2$，步长是$\gamma$，精度是$\mathcal{O}(\gamma^2)=\mathcal{O}(\alpha)$。这样一来，选定学习率$\alpha$后，在同样精度下，Momentum实际上是步长$\sqrt{\alpha}$前进的，而纯GD则是以步长$\alpha$前进的。

由于学习率一般小于1，所以$\sqrt{\alpha} > \alpha$。所以

Momentum加速的原理之一就是可以在同等学习率、不损失精度的情况下，使得整个算法以更大步长前进。

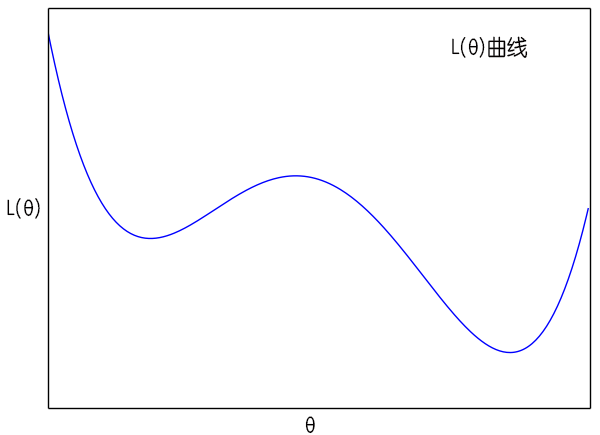
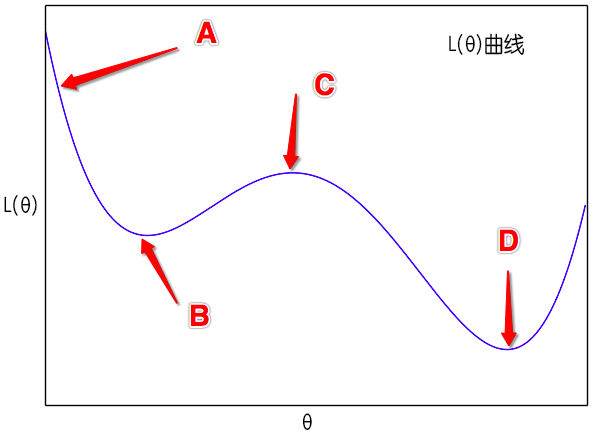
此外，如图所示，假如从$A$点出发，那么梯度下降则会慢慢降低到$B$点来，最后停留在$C$点，当然，如果噪声、学习率比较大，那么它还有可能越过$C$点从而到达$D$点。但是有了动量加速后，这时$(10)$是一个动力学方程，牛顿力学的所有东西都可以搬到这里来。从$A$点出发，开始速度为0，然后慢慢下降，势能转化为动能，然后经过$B$点后慢慢上升，动能转化为势能，如果摩擦力比较小，那么到达$C$点后还有动能，那它就能直接到达$D$点去了。这是能量守恒保证的，哪怕没有噪声也可以。而在sgd中，要靠大学习率、小batch size（增强噪声）才能达到类似的效果。

所以，我们还可以说

Momentum加速为“越过”不那么好的极小值点提供了来自动力学的可能性。

那么$\lambda$应该要怎么选呢？直接让$\lambda=0$或$\beta=1$不成吗？

前面说到，$\lambda > 0$这一项相当于摩擦力，用来消耗能量，如果没有这一项，不管学习率多小，只要不为零，那么Momentum算法不会停留在极小值点，会一直动下去。就好比如果没有摩擦力的话，单摆就会不断摆动，不会停止，这是能量守恒决定的，能量守恒告诉我们，在能量的最低点（也就是我们期望的最小值点）时，动能是最大的，也就是速度是最快的，说白了，算法是根本停不下来～～但是如果有摩擦力消耗掉能量，能量不再守恒，那么单摆最终停留在能量的最低点。所以，引入$\lambda$对算法的收敛来说是必须的，同时从$(15)$我们有$\beta < 1$。但是，$\lambda$也不能过大，过大的摩擦力会导致运动没到达最低点就停止了，为了保证加速效果的存在，我们还有$\beta > 0$。

最后，从$(15)$式的$\beta$的定义可以看到，当固定$\lambda$时（也就是固定摩擦系数），如果学习率$\alpha$降低（意味着$\gamma$也降低），那么$\beta$应该随之升高，其中提升的比例可以进行简单的估算。由$(16)$我们得到近似$1-\lambda\sqrt{\alpha}=\beta$，从而可以反解出$\lambda$，然后代入新的$\alpha$，就可以算出新的$\beta$。。

这样我们就得到，SGD+Momentum的优化器中$\beta$的一个供参考的调参方案：

在使用SGD+Momentum时，如果降低学习率，那么应当轻微提升$\beta$。当学习率从$\alpha$降到$r\alpha$时，$\beta$可以考虑提升到$1 - (1-\beta)\sqrt{r}$。

Nesterov动量 #

Momentum算法本质上在数值求解$(10)$，而求解$(10)$并不只有$(13),(14)$这种显式的迭代格式，还有隐式的迭代。比如我们可以将$(10)$近似为
$$\begin{aligned}&\frac{\boldsymbol{\theta}_{n+1}-\boldsymbol{\theta}_{n}}{\gamma} = \frac{\boldsymbol{\eta}_{n+1}+\boldsymbol{\eta}_{n}}{2}\\
&\frac{\boldsymbol{\eta}_{n+1}-\boldsymbol{\eta}_{n-1}}{2\gamma} = -\lambda \frac{\boldsymbol{\eta}_{n}+\boldsymbol{\eta}_{n-1}}{2} - \nabla_{\boldsymbol{\theta}} L\left(\frac{\boldsymbol{\theta}_{n+1}+\boldsymbol{\theta}_n}{2}\right)
\end{aligned}\tag{17}$$
设
$$\boldsymbol{v}_{n+1}=\frac{\gamma}{2}(\boldsymbol{\eta}_{n+1}+\boldsymbol{\eta}_{n}),\quad \beta = 1-\lambda\gamma,\quad \alpha=\gamma^2\tag{18}$$
就得到
$$\begin{aligned}&\boldsymbol{\theta}_{n+1} = \boldsymbol{\theta}_{n} + \boldsymbol{v}_{n+1} \\ & \boldsymbol{v}_{n+1} = \beta\boldsymbol{v}_{n} - \alpha \nabla_{\boldsymbol{\theta}} L\left(\frac{\boldsymbol{\theta}_{n+1}+\boldsymbol{\theta}_n}{2}\right) \end{aligned}\tag{19}$$
这是一种隐式的迭代公式，理论上为了求$\boldsymbol{\theta}_{n+1}$我们还需要解一个非线性方程组。但近似来看，只需要将$\boldsymbol{\theta}_{n+1}$用$\boldsymbol{\theta}_{n}+\beta \boldsymbol{v}_{n}$近似，得到
$$\begin{aligned}&\boldsymbol{\theta}_{n+1} = \boldsymbol{\theta}_{n} + \boldsymbol{v}_{n+1} \\ & \boldsymbol{v}_{n+1} = \beta\boldsymbol{v}_{n} - \alpha \nabla_{\boldsymbol{\theta}} L\left(\boldsymbol{\theta}_n + \frac{\beta}{2}\boldsymbol{v}_n\right) \end{aligned}\tag{20}$$
如果将括号里边的$\beta/2$替换成$\beta$，那么就是标准的带Nesterov动量的GD算法，然而我觉得上式似乎更加合理，因为Nesterov算法想着用$\boldsymbol{\theta}_{n+1}$处的梯度代替$\boldsymbol{\theta}_n$处的梯度，以赋予算法“前瞻能力”，但事实上还是有偏了，直觉上用$(\boldsymbol{\theta}_n+\boldsymbol{\theta}_{n+1})/2$处的梯度更加“中肯”一些。

从误差分析来看，其实不管是标准的Momentum还是Nesterov版本，都是一个二阶算法，精确度相同（只是一个常数级的差别）。但理论上Nesterov是一个隐式的迭代，稳定域更广一些，所以通常能得到更好的效果。

怎么用tf等框架实现$(20)$式呢？注意$(20)$涉及到了将$L(\boldsymbol{\theta})$先对$\boldsymbol{\theta}$求导，然后将$\boldsymbol{\theta}$替换成$\boldsymbol{\theta}_n + \frac{\beta}{2}\boldsymbol{v}_n$（我这里的Nesterov）或$\boldsymbol{\theta}_n + \beta\boldsymbol{v}_n$（标准的Nesterov），这个操作在我们看来应当是很简单的，但是在tf等框架下就有点繁琐了。

因为这些框架虽然是有自动求导功能，但它们终究只是一个数值计算框架，而不是符号计算系统，所以结果只是一个数值导数。当我们求出$\boldsymbol{\theta}$的导数时，结果是一个张量，是一些确定的数，要将$\boldsymbol{\theta}$替换成$\boldsymbol{\theta}_n + \frac{\beta}{2}\boldsymbol{v}_n$就有点难办了。当然不是不可能，但终究没有Momentum版的一步到位来得简单。

于是为了便于实现，我们设（以标准的Nesterov为例）：
$$\boldsymbol{\Theta}_n=\boldsymbol{\theta}_n + \beta\boldsymbol{v}_n$$
那么可以得到新的迭代公式：
$$\begin{aligned}&\boldsymbol{\Theta}_{n+1} = \boldsymbol{\Theta}_{n} + \beta\boldsymbol{v}_{n+1} - \alpha \nabla_{\boldsymbol{\theta}} L\left(\boldsymbol{\Theta}_n\right) \\ & \boldsymbol{v}_{n+1} = \beta\boldsymbol{v}_{n} - \alpha \nabla_{\boldsymbol{\theta}} L\left(\boldsymbol{\Theta}_n\right) \end{aligned}$$
这就是主流框架的Nesterov算法的实现方式，比如Keras的，这样就免除了自变量替换的过程。随着迭代越来越靠近极小值点，动量$\boldsymbol{v}$会越来越小，所以$\boldsymbol{\Theta}$和$\boldsymbol{\theta}$最终将会等价的——就算有一点误差也不打紧，因为我们用动量的根本目的是为了加速，而选择模型还是看valid集的效果。

Kramers方程 #

前面讨论的只是全量梯度下降的动量加速方法，最后简单分析一下随机梯度下降下的情形。跟前面一样的假设，引入随机梯度后，我们可以认为$(10)$变成了带随机力的方程
$$\ddot{\boldsymbol{\theta}} + \lambda \dot{\boldsymbol{\theta}} = - \nabla_{\boldsymbol{\theta}} L(\boldsymbol{\theta})+\sigma\boldsymbol{\xi}\tag{21}$$
这称为“Kramers方程”，跟朗之万方程一样，都是随机动力学里边的核心成果。当$\lambda=0$时，静态解可以写出来，这个静态分布可以作为一般情况下的参考：
$$P(\boldsymbol{\theta},\boldsymbol{\eta}) \sim \exp\left(-\frac{\boldsymbol{\eta}^2/2 + L(\boldsymbol{\theta})}{\sigma^2}\right)\tag{22}$$
其中$\boldsymbol{\eta}=\dot{\boldsymbol{\theta}}$，而$\boldsymbol{\theta}$的边缘分布就是$(9)$式，因此可以认为前面的纯SGD的分析在Momentum和Nesterov算法中同样成立。

思考回顾 #

本文希望通过动力学的方式来分析SGD的相关内容。对于文章开头提出的一些问题，本文并不能准确地给出答案，但我估计能够有点启发。尽管文章比较冗长，公式略多，但是本科学过数值计算的读者，应该都不难看懂的。如果有什么疑问，欢迎继续留言讨论～

转载到请包括本文地址：https://kexue.fm/archives/5655

更详细的转载事宜请参考：《科学空间FAQ》