注意力机制真的可以“集中注意力”吗？

之前在《Transformer升级之路：3、从Performer到线性Attention》、《为什么现在的LLM都是Decoder-only的架构？》等文章中，我们从Attention矩阵的“秩”的角度探讨了Attention机制，并曾经判断线性Attention不如标准Attention的关键原因正是“低秩瓶颈”。然而，这一解释对于双向的Encoder模型或许成立，但却难以适用于单向的Decoder模型，因为Decoder的Attention矩阵的上三角部分是被mask掉的，留下的下三角矩阵必然是满秩的，而既然都是满秩了，那么低秩瓶颈问题似乎就不复存在了。

所以，“低秩瓶颈”并不能完全解释线性Attention的能力缺陷。在这篇文章中，笔者试图寻求另一个角度的解释。简单来说，与标准Attention相比，线性Attention更难“集中注意力”，从而难以准确地定位到关键token，这大概是它效果稍逊一筹的主要原因。

稀疏程度 #

在文章《从熵不变性看Attention的Scale操作》中，我们就从“集中注意力”的角度考察过Attention机制，当时我们以信息熵作为“集中程度”的度量，熵越低，表明Attention越有可能集中在某个token上。

但是，对于一般的Attention机制来说，Attention矩阵可能是非归一化的，比如《FLASH：可能是近来最有意思的高效Transformer设计》介绍的GAU模块，以及《相对位置编码Transformer的一个理论缺陷与对策》所引入的$l_2$归一化Attention，甚至从更一般的Non-Local Neural Networks角度来看，Attention矩阵还未必是非负的。这些非归一化的乃至非负的Attention矩阵自然就不适用于信息熵了，因为信息熵是针对概率分布的。

为此，我们考虑在《如何度量数据的稀疏程度？》介绍的$l_1/l_2$形式的稀疏程度指标：
\begin{equation}S(x) = \frac{\mathbb{E}[|x|]}{\sqrt{\mathbb{E}[x^2]}}\end{equation}
该指标跟信息熵相似，$S(x)$越小意味着对应的随机向量越稀疏，越稀疏意味着越有可能“一家独大”，这对应于概率中的one hot分布，跟信息熵不同的是，它适用于一般的随机变量或者向量。

简化形式 #

对于注意力机制，我们记$\boldsymbol{a} = (a_1,a_2,\cdots,a_n)$，其中$a_j \propto f(\boldsymbol{q}\cdot\boldsymbol{k}_j)$，那么
\begin{equation}S(\boldsymbol{a}) = \frac{\mathbb{E}_{\boldsymbol{k}}[|f(\boldsymbol{q}\cdot\boldsymbol{k})|]}{\sqrt{\mathbb{E}_{\boldsymbol{k}}[f^2(\boldsymbol{q}\cdot\boldsymbol{k})]}}\end{equation}
接下来都考虑$n\to\infty$的极限。假设$\boldsymbol{k}\sim\mathcal{N}(\boldsymbol{\mu},\sigma^2\boldsymbol{I})$，那么可以设$\boldsymbol{k} = \boldsymbol{\mu} + \sigma \boldsymbol{\varepsilon}$，其中$\boldsymbol{\varepsilon}\sim\mathcal{N}(\boldsymbol{0},\boldsymbol{I})$，于是
\begin{equation}S(\boldsymbol{a}) = \frac{\mathbb{E}_{\boldsymbol{\varepsilon}}[|f(\boldsymbol{q}\cdot\boldsymbol{\mu} + \sigma\boldsymbol{q}\cdot\boldsymbol{\varepsilon})|]}{\sqrt{\mathbb{E}_{\boldsymbol{\varepsilon}}[f^2(\boldsymbol{q}\cdot\boldsymbol{\mu} + \sigma\boldsymbol{q}\cdot\boldsymbol{\varepsilon})]}}\end{equation}
注意$\boldsymbol{\varepsilon}$所服从的分布$\mathcal{N}(\boldsymbol{0},\boldsymbol{I})$是一个各向同性的分布，与《n维空间下两个随机向量的夹角分布》推导的化简思路一样，由于各向同性的原因，$\boldsymbol{q}\cdot\boldsymbol{\varepsilon}$相关的数学期望只与$\boldsymbol{q}$的模长有关，跟它的方向无关，于是我们可以将$\boldsymbol{q}$简化为$(\Vert\boldsymbol{q}\Vert,0,0,\cdots,0)$，那么对$\boldsymbol{\varepsilon}$的数学期望就可以简化为
\begin{equation}S(\boldsymbol{a}) = \frac{\mathbb{E}_{\varepsilon}[|f(\boldsymbol{q}\cdot\boldsymbol{\mu} + \sigma\Vert\boldsymbol{q}\Vert\varepsilon)|]}{\sqrt{\mathbb{E}_{\varepsilon}[f^2(\boldsymbol{q}\cdot\boldsymbol{\mu} + \sigma\Vert\boldsymbol{q}\Vert\varepsilon)]}}\end{equation}
其中$\varepsilon\sim\mathcal{N}(0,1)$是一个随机标量。

两个例子 #

现在可以对常见的一些$f$进行计算对比了。目前最常用的Attention机制是$f=\exp$，此时求期望只是常规的一维高斯积分，容易算得
\begin{equation}S(\boldsymbol{a}) = \exp\left(-\frac{1}{2}\sigma^2\Vert\boldsymbol{q}\Vert^2\right)\end{equation}
当$\sigma\to\infty$或$\Vert\boldsymbol{q}\Vert\to\infty$时，都有$S(\boldsymbol{a})\to 0$，也就是理论上标准Attention确实可以任意稀疏地“集中注意力”，同时这也告诉了我们让注意力更集中的方法：增大$\boldsymbol{q}$的模长，或者增大各个$\boldsymbol{k}$之间的方差，换言之拉开$\boldsymbol{k}$的差距。

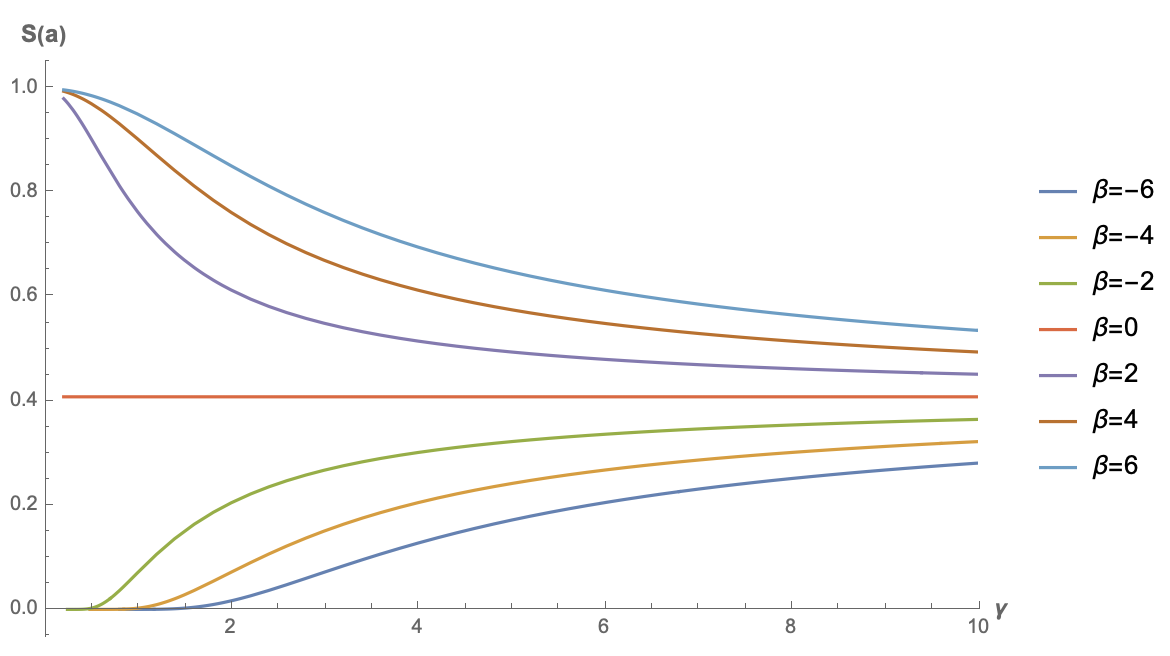
另一个例子是笔者喜欢的GAU（Gated Attention Unit），它在开始提出的时候是$f=\text{relu}^2$（不过笔者后来自己用的时候复原为Softmax了，参考《FLASH：可能是近来最有意思的高效Transformer设计》和《听说Attention与Softmax更配哦～》），此时积分没有$f=\exp$那么简单，不过也可以直接用Mathematica硬算，结果是
\begin{equation}S(\boldsymbol{a}) =\frac{e^{-\frac{\beta ^2}{2 \gamma ^2}} \left(\sqrt{2} \beta \gamma +\sqrt{\pi } e^{\frac{\beta ^2}{2 \gamma ^2}} \left(\beta ^2+\gamma ^2\right) \left(\text{erf}\left(\frac{\beta }{\sqrt{2} \gamma }\right)+1\right)\right)}{\sqrt[4]{\pi } \sqrt{2 \sqrt{2} \beta \gamma e^{-\frac{\beta ^2}{2 \gamma ^2}} \left(\beta ^2+5 \gamma ^2\right)+2 \sqrt{\pi } \left(\beta ^4+6 \beta ^2 \gamma ^2+3 \gamma ^4\right) \left(\text{erf}\left(\frac{\beta }{\sqrt{2} \gamma }\right)+1\right)}}\end{equation}
其中$\beta = \boldsymbol{q}\cdot\boldsymbol{\mu}, \gamma = \sigma\Vert\boldsymbol{q}\Vert$。式子很恐怖，但是无所谓，画图即可：

可以看到，只有$\beta < 0$时，原版GAU的稀疏度才有机会趋于0。这也很直观，当偏置项小于0时，才有更多的机会让$\text{relu}$的结果为0，从而实现稀疏。这个结果也说明了跟$f=\exp$的标准注意力不同，$\boldsymbol{k}$的bias项可能会对$f=\text{relu}^2$的GAU有正面帮助。

极简线性 #

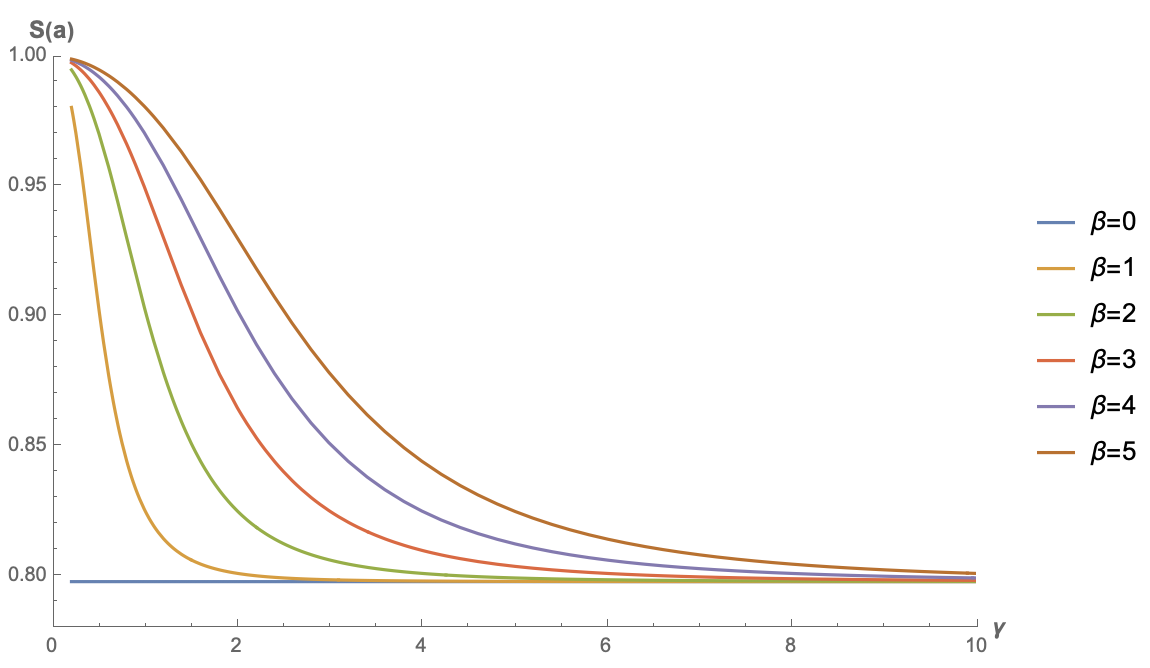
下面我们再来看一个最简单的例子：不加$f$，或者等价地说$f=\text{identical}$。这种情况下对应的就是最简单的一种线性Attention，同样可以用Mathematica硬算得：
\begin{equation}S(\boldsymbol{a}) =\frac{\sqrt{\frac{2}{\pi }} \gamma e^{-\frac{\beta ^2}{2 \gamma ^2}}+\beta \text{erf}\left(\frac{\beta }{\sqrt{2} \gamma }\right)}{\sqrt{\beta ^2+\gamma ^2}}\end{equation}
下面是几个不同$\beta$的函数图像：

注意，此时的$S(\boldsymbol{a})$是关于$\beta$偶函数（读者不妨尝试证明一下），所以$\beta < 0$时图像跟它相反数的图像是一样的，因此上图只画了$\beta \geq 0$的结果。从图中可以看出，不加任何激活函数的线性Attention的稀疏程度并不能接近0，而是存在一个较高的下限，这意味着当输入序列足够长时，这种线性Attention并没有办法“集中注意力”到关键位置上。

一般线性 #

从《线性Attention的探索：Attention必须有个Softmax吗？》我们知道，线性Attention的一般形式为$a_j \propto g(\boldsymbol{q})\cdot h(\boldsymbol{k}_j)$，其中$g,h$是值域非负的激活函数。我们记$\tilde{\boldsymbol{q}}=g(\boldsymbol{q}),\tilde{\boldsymbol{k}}=h(\boldsymbol{k})$，那么$a_j\propto \tilde{\boldsymbol{q}}^{\scriptscriptstyle\top}\tilde{\boldsymbol{k}}$，并且可以写出
\begin{equation}S(\boldsymbol{a}) = \frac{\mathbb{E}_{\boldsymbol{\varepsilon}}\left[\tilde{\boldsymbol{q}}^{\scriptscriptstyle\top}\tilde{\boldsymbol{k}}\right]}{\sqrt{\mathbb{E}_{\boldsymbol{\varepsilon}}\left[\tilde{\boldsymbol{q}}^{\scriptscriptstyle\top}\tilde{\boldsymbol{k}}\tilde{\boldsymbol{k}}^{\scriptscriptstyle\top}\tilde{\boldsymbol{q}}\right]}} = \frac{\tilde{\boldsymbol{q}}^{\scriptscriptstyle\top}\mathbb{E}_{\boldsymbol{\varepsilon}}\left[\tilde{\boldsymbol{k}}\right]}{\sqrt{\tilde{\boldsymbol{q}}^{\scriptscriptstyle\top}\mathbb{E}_{\boldsymbol{\varepsilon}}\left[\tilde{\boldsymbol{k}}\tilde{\boldsymbol{k}}^{\scriptscriptstyle\top}\right]\tilde{\boldsymbol{q}}}} = \frac{\tilde{\boldsymbol{q}}^{\scriptscriptstyle\top}\tilde{\boldsymbol{\mu}}}{\sqrt{\tilde{\boldsymbol{q}}^{\scriptscriptstyle\top}\left[\tilde{\boldsymbol{\mu}}\tilde{\boldsymbol{\mu}}^{\scriptscriptstyle\top} + \tilde{\boldsymbol{\Sigma}}\right]\tilde{\boldsymbol{q}}}} = \frac{1}{\sqrt{1 + \frac{\tilde{\boldsymbol{q}}^{\scriptscriptstyle\top}\tilde{\boldsymbol{\Sigma}}\tilde{\boldsymbol{q}}}{(\tilde{\boldsymbol{q}}^{\scriptscriptstyle\top}\tilde{\boldsymbol{\mu}})^2}}}\end{equation}
这是关于非负型线性Attention的一般结果，现在还没做任何近似，其中$\tilde{\boldsymbol{\mu}},\tilde{\boldsymbol{\Sigma}}$分别是$\tilde{\boldsymbol{k}}$序列的均值向量和协方差矩阵。

从这个结果可以看出，非负型线性Attention也可能任意稀疏（即$S(\boldsymbol{a})\to 0$），只需要均值趋于0，或者协方差趋于$\infty$，也就是说$\tilde{\boldsymbol{k}}$序列的信噪比尽可能小。然而$\tilde{\boldsymbol{k}}$序列是一个非负向量序列，信噪比很小的非负序列意味着序列中大部分元素都是相近的，于是这样的序列能表达的信息有限，也意味着线性Attention通常只能表示绝对位置的重要性（比如Attention矩阵即某一列都是1），而无法很好地表达相对位置的重要性，这本质上也是线性Attention的低秩瓶颈的体现。

为了更形象地感知$S(\boldsymbol{a})$的变化规律，我们不妨假设一种最简单的情况：$\tilde{\boldsymbol{k}}$的每一个分量是独立同分布的，这时候均值向量可以简化为$\tilde{\mu}\boldsymbol{1}$，协方差矩阵则可以简化为$\tilde{\sigma}^2\boldsymbol{I}$，那么$S(\boldsymbol{a})$的公式可以进一步简化为
\begin{equation}S(\boldsymbol{a}) = \frac{1}{\sqrt{1 + \left(\frac{\tilde{\sigma}}{\tilde{\mu}}\frac{\Vert\tilde{\boldsymbol{q}}\Vert_2}{\Vert\tilde{\boldsymbol{q}}\Vert_1}\right)^2}}\end{equation}
这个结果观察起来就更直观了，要想线性注意力变得稀疏，一个方向是增大$\frac{\tilde{\sigma}}{\tilde{\mu}}$，即降低$\tilde{\boldsymbol{k}}$序列的信噪比，另一个方向则是增大$\frac{\Vert\boldsymbol{q}\Vert_2}{\Vert\boldsymbol{q}\Vert_1}$，该因子最大值是$\sqrt{d}$，其中$d$是$\boldsymbol{q},\boldsymbol{k}$的维数，所以增大它意味着要增大$d$，而增大了$d$意味着提高了注意力矩阵的秩的上限，这跟低秩瓶颈视角的结论一样，只有增大$d$才能从根本上缓解线性Attention的不足。

特别地，我们在《Transformer升级之路：5、作为无限维的线性Attention》也分析过，标准Attention也可以理解为一种无限维的线性Attention，也就是说理论上只有将$d$增加到无穷大，才能彻底弥合两者的差距。

线性衰减 #

最后，我们来看一下在《Google新作试图“复活”RNN：RNN能否再次辉煌？》介绍过的线性RNN模型系列，它们的特点是带有一个显式的递归，这可以看成一个简单的Attention：
\begin{equation}\boldsymbol{a} = (a_1,a_2,\cdots,a_{n-1},a_n) = (\lambda^{n-1},\lambda^{n-2},\cdots,\lambda,1)\end{equation}
其中$\lambda\in(0,1]$。可以算出
\begin{equation}S(\boldsymbol{a}) = \sqrt{\frac{1 - \lambda^n}{n(1-\lambda)}\frac{1+\lambda}{1+\lambda^n}} < \sqrt{\frac{1}{n}\frac{1+\lambda}{(1-\lambda)(1+\lambda^n)}}\end{equation}
当$\lambda < 1$时，只要$n\to\infty$，总有$S(\boldsymbol{a})\to 0$，所以对于带有显式Decay的线性RNN模型来说，稀疏性是不成问题的，它的问题是只能表达随着相对位置增大而衰减的、固定不变的注意力，从而无法自适应地关注到距离足够长的Context。

文章小结 #

本文提出了通过Attention矩阵的稀疏程度来考察不同Attention机制潜力的思路，得出二次型Attention机制有可能实现任意稀疏的Attention矩阵，线性Attention则并不容易实现这种稀疏，或者只能实现绝对位置相关的稀疏，这可能是线性Attention能力有所限制的原因之一。

转载到请包括本文地址：https://www.kexue.fm/archives/9889

更详细的转载事宜请参考：《科学空间FAQ》