与向量的渊源极深的四元数

当我们在使用向量进行几何、物理研究的时候，是否曾经想到：向量竟然起源于“数”？

当向量还没有发展起来的时候（虽然“有方向有大小的量”很早就被人们认识），复数已经得到了认可并且有了初步应用。当我们把复数跟向量联系起来时，我们也许会认为，因为复平面表示的复数运算与向量有着相似之处，才把复数跟几何联系起来。然而事实却相反，向量是从对复数乃至一种称为“四元数”的东西的研究中逐渐分离出来的。换句话说，历史中出现过“四元数”与向量分别研究几何的阶段，麦克斯韦(Maxwell) 将四元 数的数量部分和矢量部分分开，作为 实 体处理，作了大量的矢量分析。三维矢量分析的建立，及同四元数的正式分裂是18世纪80年代由Gibbs和Heaviside独立完成的。矢量代数被推广到矢量函数和矢量微积分，由此开始了四元数和矢量分析的争论，最终矢量分析占了上风。因而“四元数”渐渐离开了教科书。不过，“四元数”的一些特殊而巧妙的应用，仍然使我们不至于忘记它。

什么是四元数？首先让我们来看看复数是怎么来的。众所周知，引入了$i^2=-1$之后，多得出的“虚数”与实数结合起来，就构成了复数集。但是，我们可以忽略这个说法，把复数抽象起来，变成一种纯粹的“代号”：复数是一种形式为$a+bi$的数，a,b为实数，运算时遵循实数的四则混合运算法则，当两个i相乘时，把结果记为-1，其余的情况下保持i这个代号（也就是说我们不用管i究竟是什么东西）。这样“创设”出来一种数的好处是：方便应用于研究几何和物理等问题。就是说，我们不用考虑这种数究竟代表什么，只知道这种数会方便我们，我们用它能够相对方便地得出结果，这样就行了。

当复数理论发展起来后，人们认识到，实数是一种“一维数”，也就是说一条数轴上的点就可以与所有实数一一对应，而复数是一种“二维数”，必须用到一个平面（复平面）才能够把复数与平面上的点一一对应。此时，爱尔兰的数学家哈密尔顿(William Rowan Hamilton)思考着创造出一种“三维数”，它要具有类似复数的性质，需要用三维空间来给它一一对应，它的形式为$a+bi+cj$，a,b,c为实数，其中i正是复数中的虚数单位，j是类似但独立于1和i的一个数的单位，这等价于说复数是他所构思中的“三维数”的一个子集。这样的“创造”是很简单的，我们很容易类比写出“四维数”、“五维数”，关键是这样的数能否成立。哈密尔顿要求有$j^2=-1$（但是注意$i != j$），剩下的问题就是考虑$ij=?$。

哈密尔顿给“n维数”的提出了一些要求：

“n维数”是$a_0+a_1 i_1+a_2 i_2+...+a_{n-1} i_{n-1}$的形式，其中$i_1^2=i_2^2=...=i_{n-1}^2=-1$，类似于复数中的虚数单位；它的“模”定义为$r=\sqrt{a_0^2+a_1^2+...+a_{n-1}^2}$；

通过设置普适的$i_p \cdot i_q (p != q)$结果，使得两个“n维数”的积的模，等于两个“n维数”的模的积（这一点称为“模法则”）。

满足乘法分配律。

不难发现，复数符合上述规律。哈密尔顿利用上述要求去考虑构思中的“三维数”，换句话说就是计算$ij=?$。首先得提醒读者一点，就是引入了“三维数”等这种“超复数”之后，数的运算不一定遵循我们一般所认为的法则，例如在未确认三维数的具体性质前，我们无法确定1的平方根只有$+-1$。

接着从最简单的开始，我们考虑$ij=A$，根据“模法则”，应该有|A|=1，因此不妨设$A=x+yi+(+-\sqrt{1-x^2-y^2})j$。

继续考虑$i(i+j)$，我们有：$i(i+j)=-1+ij=(-1+x)+yi+(+-\sqrt{1-x^2-y^2})j$，根据模法则，有$(-1+x)^2+y^2+(1-x^2-y^2)=(-1+x)^2+1-x^2=2$，由此计算出x=0

参考上述运算，我们已经发现了一些头绪，可以继续推算下去。同样应用模法则考虑$(1+i)(i+j)=-1+i+j+ij=(-1+x)+(y+1)i+(1+-\sqrt{1-x^2-y^2})j$，我们已经算得了x=0，代入得到$-1+(y+1)i+(1+-\sqrt{1-y^2})j$，$|(1+i)(i+j)|^2=4=(-1)^2+(y+1)^2+(1+-\sqrt{1-y^2})^2$，于是$y = +-1/sqrt{2}$。貌似我们应该欢呼了？

为了谨慎，我们再检验一个数，$(1+i)j=j+ij=x+yi+(1+-\sqrt{1-x^2-y^2})j$，代入x=0后得到$(1+i)j=yi+(1+-\sqrt{1-y^2})j$，$2=y^2+(1+-\sqrt{1-y^2})^2$，于是$y=+-1$，与上面的结果矛盾！

我们发现，这个矛盾怎么也排除不了。最终我们只能够说：“三维数”不存在！

经历了上述推导之后，你也许会感到一些悲哀：既然三维数都不存在了，那么就不用去考虑什么四维数了。然而事实却非如此，1843年10月16日，文章开头所提到的数学家哈密顿发现了目前称之为“四元数”的四维数。这是一种形式为$a+bi+cj+dk$的数。你也许会认为，令d=0，不就可以得到三维数了吗？先别着急，先看看四维数的运算法则：

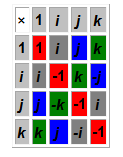
i²=j²=k²=-1

ij=k,jk=i,ki=j

ji=-k,kj=-i,ik=-j

尽管可以设d=0而令k消失，但是i和j相乘后依旧会令k出现，因而只能考虑“四元数”。这些规则都可以利用刚才我们你推导三维数时所使用的方法一一推导。并且不难发现，四元数乘法不满足交换律（AB不一定等于BA），这可以通过计算平方来推导。具体情形有兴趣的读者可以自行推导。

哈密顿在发现“四元数”的第二天给一位朋友约翰·格拉夫斯（John T Graves）写一封信报告他发现的结果。格拉夫斯根据哈密尔顿的发现由此推广到他称为“八元数”（Octaves或者Octonions）这是包含哈密尔顿四元数的另外一种新数。这种八元数，像四元数一样可以在这上面实施加、减、乘、除的运算。 哈密尔顿很高兴格拉夫斯的推广，他详细研究这八元数，发现这八元数的乘法是不满足结合律，一般来说给出三个八元数A，B，C会有A×（B×C）≠（A×B）×C的现象。 英国的数学家凯莱(Cayley)也独立发现八元数。(因为Cayley的名气较高，后人即将八元数称为Cayley数)

1844年1月4日约翰·克拉夫斯给哈密尔顿的信报告他发现的八元数基本乘法公式：

i²=j²=k²=l²=m²=n²=o²=-1

i= jk = lm = on =-kj =-ml =-no

j= ki= ln= mo= -ik= -nl= -om

k= ij =lo= nm= -ij= -ol= -mn

l=mi=nj=ok=-im=-jn=-ko

m=il=oj=kn=-li=-jo=-nk

n=jl=jo=mk=-lj=-oi=-km

o=ni=jm=kl=-in=-mj=-lk

关于四元数的实际应用，其中一个很关键的就是立体的旋转。要了解更多的内容，还可以参考本文的附件。本文章旨在对四元数的发展以及数的拓展做一个简单的描述。如果日后有机会，也一定和读者具体讨论下四元数的应用。

关于四元数，参考：http://zh.wikipedia.org/zh-cn/%E5%9B%9B%E5%85%83%E6%95%B8

关于哈密顿，参考：http://www.math123.cn/sxxs/588.htm

附件：四元数.pdf

转载到请包括本文地址：https://kexue.fm/archives/898

更详细的转载事宜请参考：《科学空间FAQ》