有限内存下全局打乱几百G文件（Python）

这篇文章我们来做一道编程题：

如何在有限内存下全局随机打乱（Shuffle）几百G的文本文件？

题目背景其实很明朗，现在预训练模型动辄就几十甚至几百G语料了，为了让模型能更好地进行预训练，对训练语料进行一次全局的随机打乱是很有必要的。但对于很多人来说，几百G的语料往往比内存还要大，所以如何能在有限内存下做到全局的随机打乱，便是一个很值得研究的问题了。

已有工具 #

假设我们的文件是按行存储的，也就是一行代表一个样本，我们要做的就是按行随机打乱文件。假设我们只有一个文件，并且这个文件大小明显小于内存，那么我们可以用linux自带的shuf命令：

shuf input.txt -o output.txt

之所以强调文件大小明显小于内存，是因为shuf会把整个文件加载到内存中再打乱的，这就要求我们有足够大的内存。针对此，一个改进版叫terashuf（链接），它通过切分文件的方式，用硬盘空间代替内存，使得我们可以打乱大于内存的文件。

看上去terashuf已经完全能满足我们的需求了。理论上确实是的，但是有时候我们可能会有很多个性化的需求，比如将多个文件混合起来随机打乱，或者将打乱后的输出切分为多个文件，等等。因此，我们最好能够自己用Python把它实现出来，以便应对更复杂的定制需求。

打乱算法 #

现在我们来看一下，在有限内存下进行全局打算的算法究竟是怎样的呢？大体上步骤如下：

1、假设文件共有$mn$行，那么分割为$m$个文件，每个文件$n$行；

2、每个$n$行的文件内部随机打乱，因为这个$n$是任意指定的，因此这步可以在内存中完成；

3、读取每个文件的第一行（得到$m$行数据），将这$m$行数据随机写入到输出文件中；

4、依次读取每个文件的第$2,\cdots,n$行，重复第3步操作。

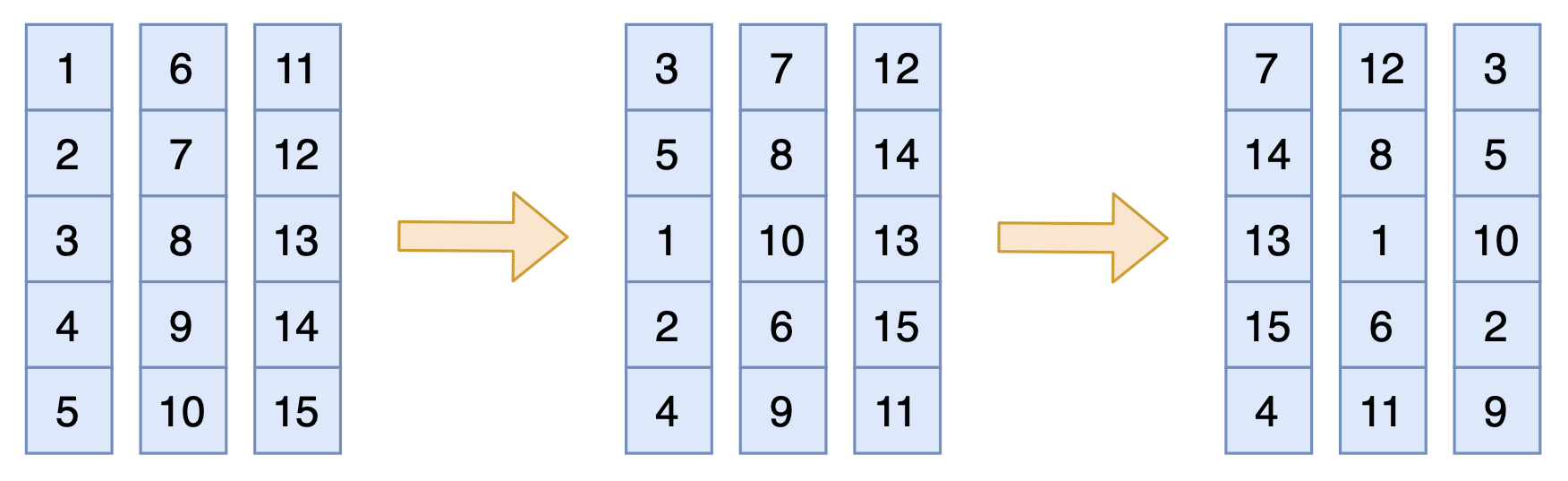
说白了，就是先竖着打乱一遍，然后横着打乱一遍，就能得到一个充分打乱的结果，接近全局打乱，如下图：

注意这样的算法只能保证得到一个尽可能乱的结果，但是无法保证任何排序都有可能出现，比如输出的前2个样本不可能正好是第1个文件的前2个样本。如果要真正实现所有排序等概率出现，需要我们每一步都按照每个文件的剩余行数来依概率采样，而不是同时读完每个文件的第$k$行再读每个文件的第$k+1$行。但每一步都依概率采样会增加采样成本，而且对于实际使用来说效果也差别不大，因此没太大必要。

实际情况下，按每个文件$n$行来分割文件时，最后一个文件可能不足$n$行，如果我们不在乎这个小细节，那么依旧可以按照上述流程执行，而最后一个文件先被读取完后，继续返回空行就好，整个流程不会报错。当然，这会导致最后一个文件的样本排序偏前，对于有强迫症的读者可能无法接受这一点，这时可以考虑在读取最后一个文件的时候，引入拒绝采样，拒绝率为$1-\frac{\text{最后一个文本剩余行数}}{\text{其余每个文本剩余行数}}$。

参考实现（没有引入拒绝采样）：

Github：https://github.com/bojone/shuffle

性能测试 #

如果只是合并、打乱、分割三种操作的结合，那么其实用shell命令加terashuf也可以实现，大致命令为

cat corpus/*.json | TMPDIR=/root/tmp MEMORY=20 ./terashuf | split -l 100000 -a 5 -d - corpus-

经比较，在同样的环境下，总大小约为280G的文件，用terashuf进行打乱的总时间大致为2.7小时，而笔者所写的Python代码运行时间大约为3.5小时。看起来Python代码也不是慢很多，还能接受，毕竟terashuf是C++写的，Python比C++慢并不丢人。

大多数情况下，这个全局打乱算法的瓶颈是磁盘IO速度，因此多进程/多线程基本上都不是特别管用。

本文小结 #

本文简单介绍了一下在有限内存下借助硬盘空间进行大文件全局打乱的思路，并给出了一个Python实现，有需要的读者可以自行派生出更复杂需求的代码。

转载到请包括本文地址：https://kexue.fm/archives/8662

更详细的转载事宜请参考：《科学空间FAQ》