梯度下降和EM算法:系出同源,一脉相承
By 苏剑林 | 2017-03-23 | 272588位读者 |PS:本文就是梳理了梯度下降与EM算法的关系,通过同一种思路,推导了普通的梯度下降法、pLSA中的EM算法、K-Means中的EM算法,以此表明它们基本都是同一个东西的不同方面,所谓“横看成岭侧成峰,远近高低各不同”罢了。
在机器学习中,通常都会将我们所要求解的问题表示为一个带有未知参数的损失函数(Loss),如平均平方误差(MSE),然后想办法求解这个函数的最小值,来得到最佳的参数值,从而完成建模。因将函数乘以-1后,最大值也就变成了最小值,因此一律归为最小值来说。如何求函数的最小值,在机器学习领域里,一般会流传两个大的方向:1、梯度下降;2、EM算法,也就是最大期望算法,一般用于复杂的最大似然问题的求解。
在通常的教程中,会将这两个方法描述得迥然不同,就像两大体系在分庭抗礼那样,而EM算法更是被描述得玄乎其玄的感觉。但事实上,这两个方法,都是同一个思路的不同例子而已,所谓“本是同根生”,它们就是一脉相承的东西。
让我们,先从远古的牛顿法谈起。
牛顿迭代法 #
给定一个复杂的非线性函数$f(x)$,希望求它的最小值,我们一般可以这样做,假定它足够光滑,那么它的最小值也就是它的极小值点,满足$f'(x_0)=0$,然后可以转化为求方程$f'(x)=0$的根了。非线性方程的根我们有个牛顿法,所以
\begin{equation}x_{n+1} = x_{n} - \frac{f'(x_n)}{f''(x_n)}\end{equation}
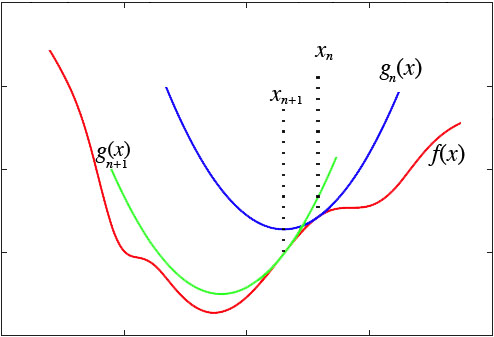
然而,这种做法脱离了几何意义,不能让我们窥探到更多的秘密。我们宁可使用如下的思路:在$y=f(x)$的$x=x_n$这一点处,我们可以用一条近似的曲线来逼近原函数,如果近似的曲线容易求最小值,那么我们就可以用这个近似的曲线求得的最小值,来近似代替原来曲线的最小值了:
显然,对近似曲线的要求是:
1、跟真实曲线在某种程度上近似,一般而言,要求至少具有一阶的近似度;
2、要有极小值点,并且极小值点容易求解。
这样,我们很自然可以选择“切抛物线”来近似:
\begin{equation}f(x)\approx g(x) = f(x_n)+f'(x_n)(x-x_n)+\frac{1}{2}f''(x_n)(x-x_n)^2\end{equation}
该抛物线具有二阶的精度。对于这条抛物线来说,极值点是
\begin{equation}x_n - \frac{f'(x_n)}{f''(x_n)}\end{equation}
所以我们重新得到了牛顿法的迭代公式:
\begin{equation}x_{n+1} = x_n - \frac{f'(x_n)}{f''(x_n)}\end{equation}
如果$f(x)$足够光滑并且在全局只有一个极值点,那么牛顿法将会是快速收敛的(速度指数增长),然而真实的函数并没有这么理想,因此,它的缺点就暴露出来了:
1、需要求二阶导数,有些函数求二阶导数之后就相当复杂了;
2、因为$f''(x_n)$的大小不定,所以$g(x)$开口方向不定,我们无法确定最后得到的结果究竟是极大值还是极小值。
梯度下降 #
这两个缺点在很多问题上都是致命性的,因此,为了解决这两个问题,我们放弃二阶精度,即去掉$f''(x_n)$,改为一个固定的正数$1/h$:
\begin{equation}g(x) = f(x_n)+f'(x_n)(x-x_n)+\frac{1}{2h}(x-x_n)^2\end{equation}
这条近似曲线只有一阶精度,但是同时也去掉了二阶导数的计算,并且保证了这是一条开口向上的抛物线,因此,通过它来迭代,至少可以保证最后会收敛到一个极小值(至少是局部最小值)。上述$g(x)$的最小值点为
\begin{equation}x_n - h f'(x_n)\end{equation}
所以我们得到迭代公式
\begin{equation}x_{n+1} = x_n - h f'(x_n)\end{equation}
对于高维空间就是
\begin{equation}\boldsymbol{x}_{n+1} = \boldsymbol{x}_n - h \nabla(\boldsymbol{x}_n)\end{equation}
这就是著名的梯度下降法了。当然,它本身存在很多问题,但很多改进的算法都是围绕着它来展开,如随机梯度下降等等。
这里我们将梯度下降法理解为近似抛物线来逼近得到的结果,既然这样子看,读者应该也会想到,凭啥我一定要用抛物线来逼近,用其他曲线来逼近不可以吗?当然可以,对于很多问题来说,梯度下降法还有可能把问题复杂化,也就是说,抛物线失效了,这时候我们就要考虑其他形式的逼近了。事实上,其他逼近方案,基本都被称为EM算法,恰好就只排除掉了系出同源的梯度下降法,实在让人不解。
最大似然 #
在估算概率的时候,我们通常的优化目标是最大似然函数,而不是MSE。比如,我们要做语言模型,就要估计任意两个词$x,y$的共现概率$p(x,y)$,假设在一个规模为$N$的语料库中,$x,y$共现的次数为$\#(x,y)$,那么我们可以得到统计结果
\begin{equation}\tilde{p}(x,y)=\frac{\#(x,y)}{N}\end{equation}
这当然是一个最基本的结果,但是会存在稀疏性问题,而且要为任意两个词语对都存一个结果,内存也基本吃不消。
更加好的解决方案是,假定$p(x,y)$可以用一个带有未知参数$\theta$($\theta$可能是向量)的函数$p(x,y;\theta)$来表示(比如神经网络),也就是然后想办法优化参数就行了。那么问题来了,优化目标是什么呢?要注意如果用MSE,最大的问题是没法保证最后得到的结果一定是非负的,而概率一定是非负的。
针对概率问题,统计学家提出了一个更加自然的方案——最大似然函数。哲学家常说“存在就是合理”的,最大似然函数的思想更加彻底,它说“存在就是最合理的”,假如$x,y$共现的次数为$\#(x,y)$,那么这个事件既然发生了,它必然是最合理的,因此概率函数
\begin{equation}\prod_{x,y} p(x,y;\theta)^{\#(x,y)}\end{equation}
取最大值,取对数后就是
\begin{equation}\sum_{x,y} \#(x,y)\log p(x,y;\theta)\end{equation}
我们应该最大化这个函数,这个函数就叫做最大似然函数。显然,$\#(x,y)$可以换成统计频率$\tilde{p}(x,y)$,结果是等价的:
\begin{equation}\sum_{x,y} \tilde{p}(x,y)\log p(x,y;\theta)\end{equation}
事实上,将它乘以负-1,得到
\begin{equation}S=-\sum_{x,y} \tilde{p}(x,y)\log p(x,y;\theta)\end{equation}
我们给它起了一个特别的名字——交叉熵,它是机器学习的一个常见的损失函数。也就是说,求最大似然函数的最大值,等价于求交叉熵的最小值。如果不预先给定$p(x,y;\theta)$的具体形式,而是直接估算$p(x,y;\theta)$,那么不难算得$p(x,y;\theta)=\tilde{p}(x,y)$,这正是我们所期望的,也说明了最大似然函数作为优化目标的合理性。
EM算法 #
对于交叉熵的优化,我们通常也会尝试用梯度下降法。但很多情况下,梯度下降并不有效,我们更愿意使用EM算法,它被称为上帝的算法。
还是以前面的语言模型为例,为了使得估计的结果泛化能力更加好,我们将$p(x,y)$变换为$p(x|y)p(y)$,然后将$p(x|y)$分解为$p(x|y)=\sum_z p(x|z)p(z|y)$,这样分解的意义,在文章《SVD分解(二):为什么SVD意味着聚类?》已经提到过,$z$可以理解为类别,或者主题,$p(x|y)$就是$y$后面接$x$的概率,而$p(z|y)$就是$y$属于主题$z$的概率,而$p(x|z)$可以理解为主题$z$里边出现$x$的概率。一般来说$z$的数目要比$x,y$的数目要少得多,从而减少参数总量。
这时候,交叉熵为
\begin{equation}S=-\sum_{x,y} \tilde{p}(x,y)\log \sum_z p(x|z)p(z|y)p(y)\end{equation}
可以认为$p(y)$可以由$\tilde{p}(y)$精确估计,因此这一项只是贡献一个常数,所以等价的优化目标是:
\begin{equation}S=-\sum_{x,y} \tilde{p}(x,y)\log \sum_z p(x|z)p(z|y)\end{equation}
这里的$p(x|z),p(z|y)$都是待求参数(遍历所有可能的x,y,z组合)。
它的梯度是
\begin{equation}\begin{aligned}&\frac{\partial S}{\partial p(x|z)} = -\sum_{y} \frac{\tilde{p}(x,y)}{\sum_z p(x|z)p(z|y)}p(z|y)\\
&\frac{\partial S}{\partial p(z|y)} = -\sum_{x} \frac{\tilde{p}(x,y)}{\sum_z p(x|z)p(z|y)}p(x|z)\end{aligned}\end{equation}
直接梯度下降是行不通的,因为这里$p(x|z),p(z|y)$都是非负数,并且满足约束
\begin{equation}\sum_x p(x|z) = 1,\quad \sum_z p(z|y)=1\end{equation}
梯度下降没法保证非负数约束,这注定了它无法有效解决此类问题。我们回顾文章开始推导梯度下降的思路,是用近似曲线代替原曲线来迭代,梯度下降使用的是抛物线近似,这里我们不使用抛物线近似(因为它不能保证正定约束),而是想办法构造新的近似。假设我们已经进行了$n$次迭代,得到估计$p_n(x|z),p_n(z|y)$,那么根据梯度公式,本次的梯度为
\begin{equation}\begin{aligned}&\frac{\partial S}{\partial p_n(x|z)} = -\sum_{y} \frac{\tilde{p}(x,y)}{\sum_z p_n(x|z)p_n(z|y)}p_n(z|y)\\
&\frac{\partial S}{\partial p_n(z|y)} = -\sum_{x} \frac{\tilde{p}(x,y)}{\sum_z p_n(x|z)p_n(z|y)}p_n(x|z)\end{aligned}\end{equation}
原问题的难度就在于,$\log$里边还带有求和,如果能把求和放到外边就简单了,因此,我们不妨考虑这样的近似函数
\begin{equation}S_n'=-\sum_{x,y} \tilde{p}(x,y)\sum_z C_{x,y,z,n} \log p(x|z)p(z|y)\end{equation}
其中$C$是一个常数(在本次迭代),这样$S_n'$也具有最小值,并且可以精确求解出来。自然,我们希望$S'$的梯度跟原来$S$的梯度是一样的(具有一阶精度)。$S'$的梯度是
\begin{equation}\begin{aligned}&\frac{\partial S'}{\partial p_n(x|z)} = -\sum_{y} \frac{\tilde{p}(x,y)C_{x,y,z,n}}{p_n(x|z)}\\
&\frac{\partial S'}{\partial p_n(z|y)} = -\sum_{x} \frac{\tilde{p}(x,y)C_{x,y,z,n}}{p_n(z|y)}\end{aligned}\end{equation}
对比两组梯度,就可以得到
\begin{equation}C_{x,y,z,n}=\frac{p_n(x|z)p_n(z|y)}{\sum_z p_n(x|z)p_n(z|y)}\end{equation}
也就是说,当我们有了一组初始参数之后,可以代入上式求出$C_{x,y,z,n}$,然后求$S_n'$取最小值的参数作为$p_{n+1}(x|z)$和$p_{n+1}(z|y)$,如此迭代下去。
这部分内容,基本就是pLSA模型的求解过程,后面的细节可以参考《自然语言处理之PLSA》。对于本文来说,这里就是要指出,EM算法跟梯度下降一样,系出同源,都是基于近似曲线逼近的,并非什么玄乎的方法,并且这个近似函数的寻找,是有根有据的。而网上几乎所有的教程,都是直接地给出$S'$的表达式(一般的教程称为Q函数),以一种我感觉像是玄学的方式来讲解这个函数,让我非常反感。
K-Means #
K-Means聚类很容易理解,就是已知$N$个点的坐标$\boldsymbol{x}_i,\,i=1,\dots,N$,然后想办法将这堆点分为$K$类,每个类有一个聚类中心$\boldsymbol{c}_j,\,j=1,\dots,K$,很自然地,一个点所属的类别,就是跟它最近的那个聚类中心$\boldsymbol{c}_j$所代表的类别,这里的距离定义为欧式距离。
所以,K-Means聚类的主要任务就是求聚类中心$\boldsymbol{c}_j$。我们当然希望每个聚类中心正好就在类别的“中心”了,用函数来表示出来,就是希望下述函数$L$最小:
\begin{equation}L=\sum_{i=1}^N \min\bigg\{|\boldsymbol{x}_i-\boldsymbol{c}_1|^2,|\boldsymbol{x}_i-\boldsymbol{c}_2|^2,\dots,|\boldsymbol{x}_i-\boldsymbol{c}_K|^2\bigg\}\end{equation}
其中,$\min$操作保证了每个点只属于离它最近的那一类。
如果直接用梯度下降法优化$L$,那么将会遇到很大困难,不过这倒不是因为$\min$操作难以求导,而是因为这是一个NP的问题,理论收敛时间随着$N$成指数增长。这时我们也是用EM算法的,这时候EM算法表现为:
1、随机选$K$个点作为初始聚类中心;
2、已知$K$个聚类中心的前提下,算出各个点分别属于哪一类,然后用同一类的所有点的平均坐标,来作为新的聚类中心。
这种方法迭代几次基本就能够收敛了,那么,这样做的理由又在哪儿呢?
我们依旧是近似曲线逼近的思路,但问题是,现在的$\min$不可导怎么办呢?可以考虑用光滑近似,然后再取极限,答案在这里:《寻求一个光滑的最大值函数》。取一个足够大的$M$,那么就可以认为(最小值等于相反数的最大值的相反数)
\begin{equation}\begin{aligned}&\min\bigg\{|\boldsymbol{x}_i-\boldsymbol{c}_1|^2,|\boldsymbol{x}_i-\boldsymbol{c}_2|^2,\dots,|\boldsymbol{x}_i-\boldsymbol{c}_K|^2\bigg\}\\
=&-\frac{1}{M}\ln\bigg(e^{-M|\boldsymbol{x}_i-\boldsymbol{c}_1|^2}+e^{-M|\boldsymbol{x}_i-\boldsymbol{c}_2|^2}+\dots+e^{-M|\boldsymbol{x}_i-\boldsymbol{c}_K|^2}\bigg)\end{aligned}\end{equation}
这时候
\begin{equation}L=-\sum_{i=1}^N \frac{1}{M}\ln\bigg(e^{-M|\boldsymbol{x}_i-\boldsymbol{c}_1|^2}+e^{-M|\boldsymbol{x}_i-\boldsymbol{c}_2|^2}+\dots+e^{-M|\boldsymbol{x}_i-\boldsymbol{c}_K|^2}\bigg)\end{equation}
就可以求梯度了:
\begin{equation}\frac{\partial L}{\boldsymbol{c}_j}=\sum_{i=1}^N \frac{2e^{-M|\boldsymbol{x}_i-\boldsymbol{c}_j|^2 } }{e^{-M|\boldsymbol{x}_i-\boldsymbol{c}_1|^2}+e^{-M|\boldsymbol{x}_i-\boldsymbol{c}_2|^2}+\dots+e^{-M|\boldsymbol{x}_i-\boldsymbol{c}_K|^2}}(\boldsymbol{c}_j-\boldsymbol{x}_i)\end{equation}
设第$n$次迭代的结果为$\boldsymbol{c}^{(n)}_j$,那么该轮的梯度就是:
\begin{equation}\frac{\partial L}{\boldsymbol{c}^{(n)}_j}=\sum_{i=1}^N \frac{2e^{-M|\boldsymbol{x}_i-\boldsymbol{c}^{(n)}_j|^2 } }{e^{-M|\boldsymbol{x}_i-\boldsymbol{c}^{(n)}_1|^2}+e^{-M|\boldsymbol{x}_i-\boldsymbol{c}^{(n)}_2|^2}+\dots+e^{-M|\boldsymbol{x}_i-\boldsymbol{c}_K^{(n)}|^2}}(\boldsymbol{c}^{(n)}_j-\boldsymbol{x}_i)\end{equation}
根据这个式子的特点,我们可以寻找这样的近似曲线(应该是超曲面了):
\begin{equation}L'=\sum_{i=1}^N \sum_{j=1}^K C^{(n)}_{i,j} |\boldsymbol{x}_i-\boldsymbol{c}_j|^2 \end{equation}
其中$C^{(n)}_{i,j}$待定,它在每一轮都是一个常数,所以这只是一个二次函数,不难求得它的最小值点是
\begin{equation}\boldsymbol{c}_j = \frac{\sum_{i=1}^N C^{(n)}_{i,j}\boldsymbol{x}_i}{\sum_{i=1}^N C^{(n)}_{i,j}}\end{equation}
即$\boldsymbol{x}_i$的加权平均。
同样地,我们希望它这个近似曲线跟原函数比,至少具有一阶近似,因此我们求它的导数:
\begin{equation}\frac{\partial L'}{\boldsymbol{c}_j}=\sum_{i=1}^N 2C^{(n)}_{i,j} (\boldsymbol{c}_j-\boldsymbol{x}_i)\end{equation}
对比原函数的导数,不难得到
\begin{equation}C^{(n)}_{i,j} = \frac{e^{-M|\boldsymbol{x}_i-\boldsymbol{c}^{(n)}_j|^2 } }{e^{-M|\boldsymbol{x}_i-\boldsymbol{c}^{(n)}_1|^2}+e^{-M|\boldsymbol{x}_i-\boldsymbol{c}^{(n)}_2|^2}+\dots+e^{-M|\boldsymbol{x}_i-\boldsymbol{c}_K^{(n)}|^2}}\end{equation}
这时候我们就得到迭代公式:
\begin{equation}\boldsymbol{c}^{(n+1)}_j = \frac{\sum_{i=1}^N C^{(n)}_{i,j}\boldsymbol{x}_i}{\sum_{i=1}^N C^{(n)}_{i,j}}\end{equation}
至此,我们对各个步骤都推导完毕,但我们还是使用连续近似,最后我们要取$M\to\infty$的极限了,取极限后问题可以化简。由上式可以推得:
\begin{equation}\lim_{M\to\infty} C^{(n)}_{i,j} = \Delta^{(n)}_{i,j} = \left\{\begin{aligned}&1,\text{对于固定的i,j到i的距离最小}\\
&0,\text{其它情况}\end{aligned}\right.\end{equation}
说白了,将$\Delta^{(n)}_{i,j}$看成是$N$行$K$列的矩阵,那么矩阵的每一行只能有一个1,其它都是0;如果第$i$行中是第$j$个元素为1,就意味着距离$\boldsymbol{x}_i$最近的类别中心为$\boldsymbol{c}_j$。这时候,迭代公式变为
\begin{equation}\boldsymbol{c}^{(n+1)}_j = \frac{\sum_{i=1}^N \Delta^{(n)}_{i,j}\boldsymbol{x}_i}{\sum_{i=1}^N \Delta^{(n)}_{i,j}}\end{equation}
根据$\Delta^{(n)}_{i,j}$的含义,这无外乎就是说:
$\boldsymbol{c}^{(n+1)}_j$就是距离$\boldsymbol{c}^{(n)}_j$最近的那些点的平均值。
这就得到了通常我们在求解K-Means问题时所用的迭代算法了,它也被称为EM算法。
总结 #
可以看到,所谓EM算法,并不是一个特定的方法,而是一类方法,或者说一种策略,而梯度下降法本来也就是这类方法中的一个特例,完全是一回事,严格来讲不应该排除它。所谓上帝算法,其实就是迭代法,通过自身的迭代更新可以趋于完美(最优解),这如同生物进化般完美,好比造物者精心设计般,无怪乎被称为上帝算法了。
转载到请包括本文地址:https://www.kexue.fm/archives/4277
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Mar. 23, 2017). 《梯度下降和EM算法:系出同源,一脉相承 》[Blog post]. Retrieved from https://www.kexue.fm/archives/4277
@online{kexuefm-4277,
title={梯度下降和EM算法:系出同源,一脉相承},
author={苏剑林},
year={2017},
month={Mar},
url={\url{https://www.kexue.fm/archives/4277}},
}










August 16th, 2020
公式14到15的变换有些奇怪。$p(y)$直接拿掉不对吧?即使可以估计$p(y)$,顶多是把它拿到第一层求和号外面,而不是当作常数去掉?
$$\begin{aligned}&\sum_{x,y} \tilde{p}(x,y)\log \sum_z p(x|z)p(z|y)p(y)\\
=&\sum_{x,y} \tilde{p}(x,y)\log \left(p(y)\sum_z p(x|z)p(z|y)\right)\\
=&\sum_{x,y} \tilde{p}(x,y)\left(\log p(y)+\log\sum_z p(x|z)p(z|y)\right)\\
=&\sum_{x,y} \tilde{p}(x,y)\log p(y)+\sum_{x,y}\tilde{p}(x,y)\log\sum_z p(x|z)p(z|y)\\
=&\text{常数} +\sum_{x,y}\tilde{p}(x,y)\log\sum_z p(x|z)p(z|y)
\end{aligned}$$
August 22nd, 2020
苏神,有个问题想问一下,关于公式16里面的记号x、y、z重复的比较多,感觉有点乱,看不太懂,可以详细解释一下吗?麻烦您了!
又明白了~~~
August 22nd, 2020
苏神,请问公式19的最小值怎么解呢?
直接求导解决
August 23rd, 2020
苏神您好,公式17您说梯度下降没法保证非负数约束,可是EM是如何保证非负数约束的呢?
EM算法将优化目标换成了一个近似的目标,然后求近似目标的精确解。近似目标同样带$\log$,比如$(19)$式,既然带$\log$,那么它的最优解就不可能为负的。
April 17th, 2022
苏神您好, 拜读了之后很有收获, 但是有一点不是很理解的地方.
按照我对文章的理解, 公式(19)中构造了$S_n'$, 并保证它和$S_n$的一阶导是相同的. 接下来通过$S_n'$的一阶导找到其极小值$p_{n+1}$, 从而得到了第$n+1$次迭代的参数.
但是有一点, 既然我们已经保证了$S_n'$和$S_n$有相同的一阶导, 且之后求解$S_n'$的极小值时也只使用了其一阶导, 那我们是不是没必要构造这样一个$S_n'$, 直接令$S_n$的一阶导为$0$即可. (当然这里构造$S_n'$可以帮助理解为什么EM和GD系出同源, 但构造它是不是对于求解并没有帮助.)
你说的也没错,这本质上就是求$S$的一阶导数,然后用迭代法求解一阶导数等于0的方程组。但具体写出$S'$的好处在于,我们可以分析$S'$本身的凸性,确定它是否有全局最优点等,这能帮助我们判断迭代格式是否能收敛,以及收敛结果是最大值点还是最小值点。
June 3rd, 2022
(19),(27)的构造近似表达式,有没有固定的套路?如果没有,文中的方法并没有实用的价值。
相反,一般介绍EM的文章中的Q函数的设计是有套路可寻的。另外,文中19,27式,是否根据Q函数反推的呢?
1、EM算法的设计没有固定的套路,所谓Q函数,只不过是EM算法的一个特例,并不代表所有EM算法;
2、按照本文的视角,EM算法是本文的一个特例,既然你说EM算法有套路,那么本文就有套路;
3、文章是希望提供一个联系各个算法的视角,你说从Q函数反推,这其实也没错,但从Q函数反推之后,也可以将反推的结果作为新的出发点,去推导Q函数。
August 19th, 2022
苏神, 公式$(1)$,你应该指的是用直线近似的牛顿法吧,所以是不是该写成$x_{n+1} = x_n-\frac{f(x_n)}{f'(x_n)}$ 呢? (评论总被吞)
你没看清楚,要解的方程是$f'(x)=0$而不是$f(x)=0$。
October 19th, 2022
[...]梯度下降和EM算法:系出同源,一脉相承[...]
January 6th, 2023
在这里问一个可能会被笑话的问题。。
这些推导公式里面的log没有写底的话 一般默认是以多少为底的呀?
e
原来如此 谢谢!
February 28th, 2024
感觉本文讲的其实是MM算法的思想,可以说EM和梯度下降等都是MM算法的特例.
参考Probabilistic Machine Learning: Advanced Topics, Bound Optimization (MM) algorithm那一章
说的是Majorize-Minimize?之前没听说这个名字,搜索了一下确实是同样的意思。