OCR技术浅探：3. 特征提取(1)

作为OCR系统的第一步，特征提取是希望找出图像中候选的文字区域特征，以便我们在第二步进行文字定位和第三步进行识别. 在这部分内容中，我们集中精力模仿肉眼对图像与汉字的处理过程，在图像的处理和汉字的定位方面走了一条创新的道路. 这部分工作是整个OCR系统最核心的部分，也是我们工作中最核心的部分.

传统的文本分割思路大多数是“边缘检测 + 腐蚀膨胀 + 联通区域检测”，如论文[1]. 然而，在复杂背景的图像下进行边缘检测会导致背景部分的边缘过多(即噪音增加)，同时文字部分的边缘信息则容易被忽略，从而导致效果变差. 如果在此时进行腐蚀或膨胀，那么将会使得背景区域跟文字区域粘合，效果进一步恶化.（事实上，我们在这条路上已经走得足够远了，我们甚至自己写过边缘检测函数来做这个事情，经过很多测试，最终我们决定放弃这种思路。）

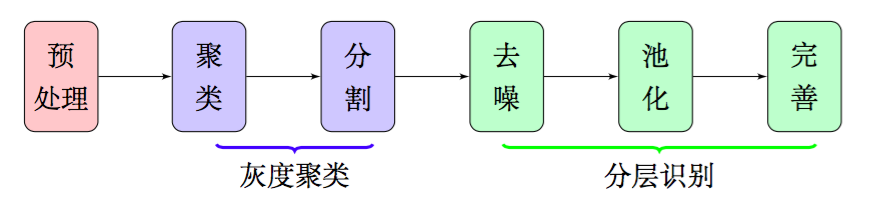
因此，在本文中，我们放弃了边缘检测和腐蚀膨胀，通过聚类、分割、去噪、池化等步骤，得到了比较良好的文字部分的特征，整个流程大致如图2，这些特征甚至可以直接输入到文字识别模型中进行识别，而不用做额外的处理.由于我们每一部分结果都有相应的理论基础作为支撑，因此能够模型的可靠性得到保证.

在这部分的实验中，我们以图3来演示我们的效果. 这个图像的特点是尺寸中等，背景较炫，色彩较为丰富，并且文字跟图片混合排版，排版格式不固定，是比较典型的电商类宣传图片. 可以看到，处理这张图片的要点就是如何识别图片区域和文字区域，识别并剔除右端的电饭锅，只保留文字区域.

图像的预处理 #

首先，我们将原始图片以灰度图像的形式读入，得到一个$m\times n$的灰度矩阵$M$，其中$m,n$是图像的长、宽. 这样读入比直接读入RGB彩色图像维度更低，同时没有明显损失文字信息. 转换为灰度图事实上就是将原来的RGB图像的三个通道以下面的公式整合为一个通道：
$$Y = 0.299R+0.587 G+0.114 B\tag{1}$$
图3的灰度图如下图.

图像本身的尺寸不大，如果直接处理，则会导致文字笔画过小，容易被当成噪音处理掉，因此为了保证文字的笔画有一定的厚度，可以先将图片进行放大. 在我们的实验中，一般将图像放大为原来的两倍就有比较好的效果了.

不过，图像放大之后，文字与背景之间的区分度降低了. 这是因为图片放大时会使用插值算法来填补空缺部分的像素. 这时候需要相应地增大区分度. 经过测试，在大多数图片中，使用次数为2的“幂次变换”效果较好. 幂次变换为
$$x \mapsto x^r\tag{2}$$
其中$x$代表矩阵$M$中的元素，$r$为次数，在这里我们选取为2. 然后需要将结果映射到$[0,255]$区间：
$$x \mapsto \frac{x-M_{min}}{M_{max}-M_{min}}\times 255\tag{3}$$
其中$M_{max},M_{min}$是矩阵$M$的最大值和最小值. 经过这样处理后，图像如下图.

灰度聚类 #

接着我们就对图像的色彩进行聚类. 聚类的有两个事实依据：

1. 灰度分辨率 肉眼的灰度分辨率大概为40，因此对于像素值254和255，在我们肉眼看来都只是白色；
2. 设计原则 根据我们一般的审美原则，在考虑海报设计、服装搭配等搭配的时候，一般要求在服装、海报等颜色搭配不超过三种颜色.

更通俗地说，虽然灰度图片色阶范围是$[0,255]$，但我们能感觉到的整体的色调一般不多，因此，可以将相近的色阶归为一类，从而减少颜色分布，有效地降低噪音.

事实上，聚类是根据图像的特点自适应地进行多值化的过程，避免了传统的简单二值化所带来的信息损失. 由于我们需要自动地确定聚类数目，因此传统的KMeans等聚类方法被我们抛弃了，而且经过我们测试，诸如MeanShift等可行的聚类方法又存在速度较慢等缺陷. 因此，我们自行设计了聚类方法，使用的是“核概率密度估计”的思路，通过求颜色密度极值的方式来聚类.

核密度估计

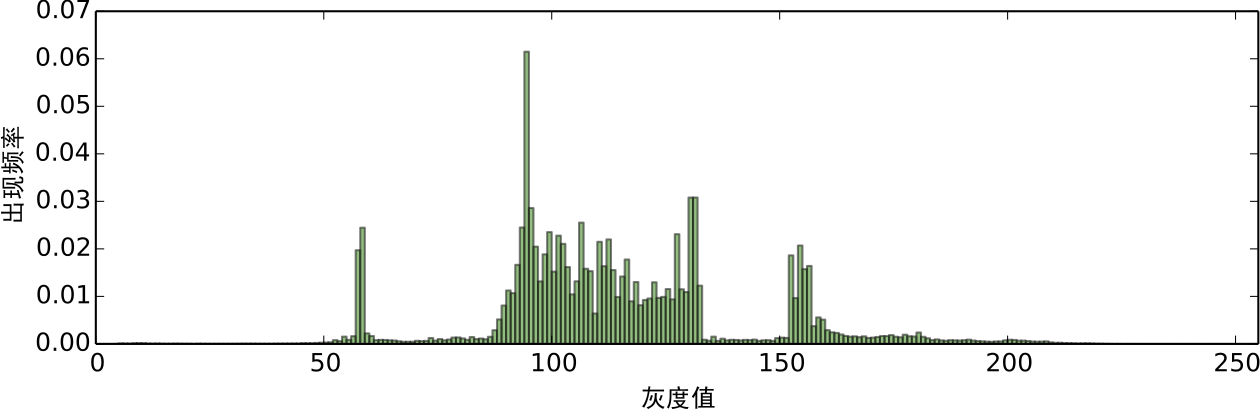
经过预处理的图像，我们可以对每个色阶的出现次数进行统计，得到如图5的频率分布直方图：

可以看到，色阶的分布形成了几个比较突出的峰，换言之，存在一定的聚类趋势. 然而，直方图的统计结果是不连续的，一个平滑的结果更便于我们分析研究，结果也更有说服力. 将统计结果平滑化的方法，就是核密度估计(kernel density estimation).

核密度估计方法是一种非参数估计方法，由Rosenblatt和Parzen提出，在统计学理论和应用领域均受到高度的重视[2]. 当然，也可以简单地将它看成一种函数平滑方式. 我们根据大量的数据来估计某个值出现的概率(密度)时，事实上做的是如下估算：
$$\hat{p}(x)=\frac{1}{nh}\sum_{i=1}^n K\left(\frac{x-x_i}{h}\right)\tag{4}$$
其中$K(x)$称为核函数. 当$h$取为1，且$K(x)$取
$$K\left(x\right)=\left\{\begin{aligned}&1,\,x=0\\
&0,\,x \neq 0\end{aligned}\right.\tag{5}$$
时，就是我们上述的直方图估计. $K(x)$这一项的含义很简单，它就是告诉我们在范围$h$内的$x_i$都算入到$x$中去，至于怎么算，由$K\left(\frac{x-x_i}{h}\right)$给出. 可见，$h$的选择对结果的影响很大，$h$我们称之为带宽(bandwidth)，它主要影响结果的平滑性.

如果$K(x)$是离散的，得到的结果还是离散的，但如果$K(x)$是光滑的，得到的结果也是比较光滑的. 一个常用的光滑函数核是高斯核：
$$K(x)=\frac{1}{\sqrt{2\pi}}e^{-x^2/2}\tag{6}$$
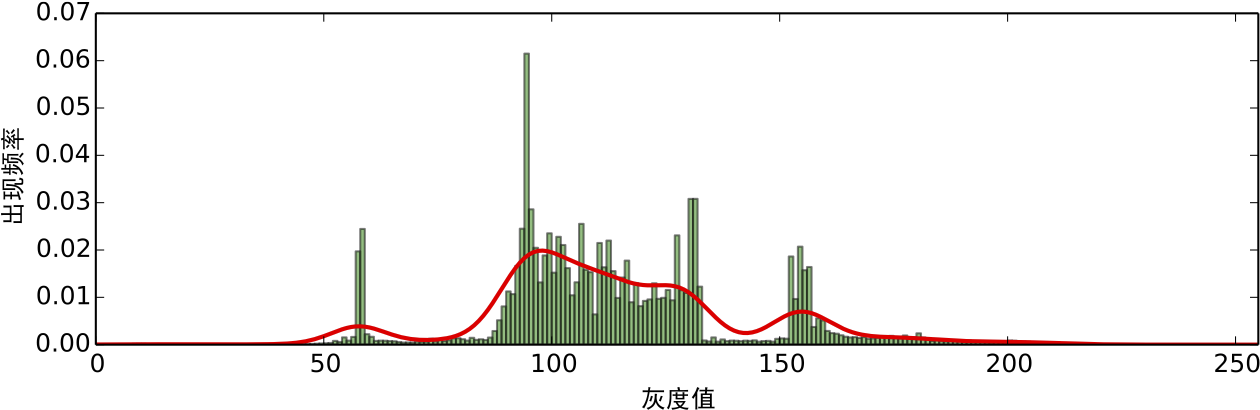
所得到的估计也叫高斯核密度估计. 在这里，我们使用scott规则自适应地选取$h$，但需要手动指定一个平滑因子，在本文中，我们选取为0.2.对于示例图片，我们得到如图6的红色曲线的结果.

极大极小值分割

从图6中我们进一步可以看出，图像确实存在着聚类趋势. 这表现为它有几个明显的极大值和极小值点，这里的极大值点位于$x=10, 57, 97, 123, 154$，极小值点位于$25, 71, 121, 142$.

因此，一个很自然的聚类方法是：有多少个极大值点，就聚为多少类，并且以极小值点作为类别之间的边界. 也就是说，对于图3，可以将图像分层5层，逐层处理. 分层之后，每一层的形状如下图，其中白色是1，黑色是0.

通过聚类将图像分为5个图层

可见，由于“对比度”和“渐变性”假设，通过聚类确实可以将文字图层通过核密度估计的聚类方法分离开来. 而且，通过聚类分层的思路，无需对文字颜色作任何假定，即便是文字颜色跟背景颜色一致时，也可以获得有效检测.

转载到请包括本文地址：https://kexue.fm/archives/3785

更详细的转载事宜请参考：《科学空间FAQ》