低精度Attention可能存在有偏的舍入误差
By 苏剑林 | 2025-10-27 | 27107位读者 | 引用前段时间笔者在arXiv上刷到了论文《Why Low-Precision Transformer Training Fails: An Analysis on Flash Attention》,里面描述的实验现象跟我们在训练Kimi K2时出现的一些现象很吻合,比如都是第二层Attention开始出现问题。论文将其归因为低精度Attention固有的有偏误差,这个分析角度是比较出乎笔者意料的,所以饶有兴致地阅读了一番。
然而,论文的表述似乎比较让人费解——当然也有笔者本就不大熟悉低精度运算的原因。总之,经过多次向作者请教后,笔者才勉强看懂论文,遂将自己的理解记录在此,供大家参考。
结论简述
要指出的是,论文标题虽然点名了“Flash Attention”,但按照论文的描述,即便block_size取到训练长度那么大,相同的问题依然会出现,所以Flash Attention的分块计算并不是引起问题的原因,因此我们可以按照朴素的低精度Attention实现来简化分析。
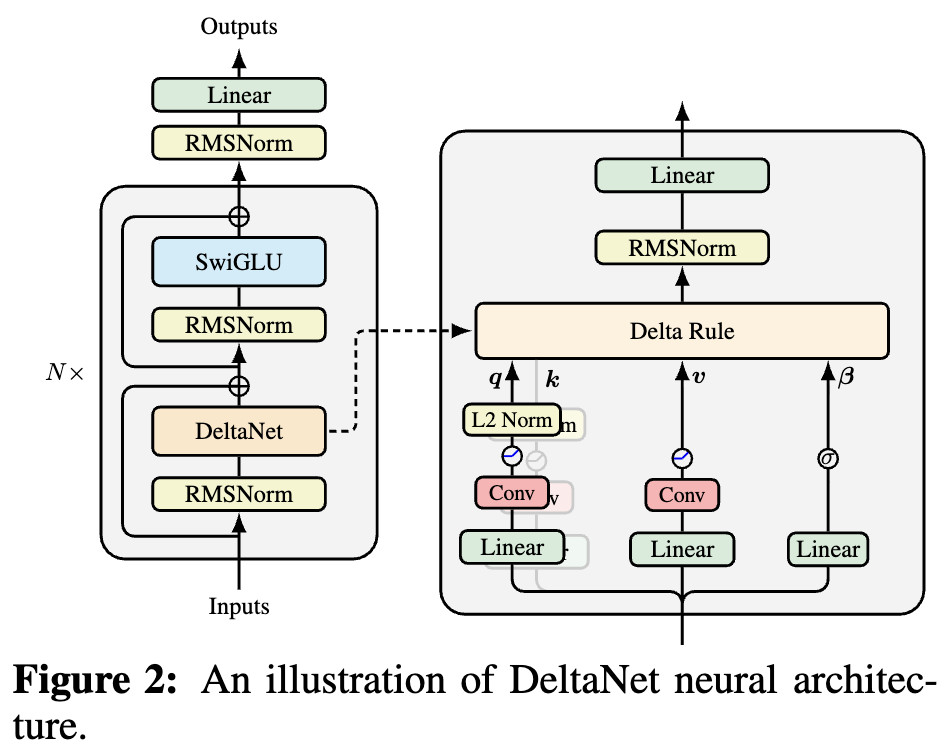
为什么线性注意力要加Short Conv?
By 苏剑林 | 2025-10-05 | 38817位读者 | 引用如果读者有关注模型架构方面的进展,那么就会发现,比较新的线性Attention(参考《线性注意力简史:从模仿、创新到反哺》)模型都给$\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}$加上了Short Conv,比如下图所示的DeltaNet:
为什么要加这个Short Conv呢?直观理解可能是增加模型深度、增强模型的Token-Mixing能力等,说白了就是补偿线性化导致的表达能力下降。这个说法当然是大差不差,但它属于“万能模版”式的回答,我们更想对它的生效机制有更准确的认知。
接下来,笔者将给出自己的一个理解(更准确说应该是猜测)。
QK-Clip:让Muon在Scaleup之路上更进一步
By 苏剑林 | 2025-07-12 | 86358位读者 | 引用四个月前,我们发布了Moonlight,在16B的MoE模型上验证了Muon优化器的有效性。在Moonlight中,我们确认了给Muon添加Weight Decay的必要性,同时提出了通过Update RMS对齐来迁移Adam超参的技巧,这使得Muon可以快速应用于LLM的训练。然而,当我们尝试将Muon进一步拓展到千亿参数以上的模型时,遇到了新的“拦路虎”——MaxLogit爆炸。
为了解决这个问题,我们提出了一种简单但极其有效的新方法,我们称之为“QK-Clip”。该方法从一个非常本质的角度去看待和解决MaxLogit现象,并且无损模型效果,这成为我们最新发布的万亿参数模型“Kimi K2”的关键训练技术之一。
问题描述
我们先来简单介绍一下MaxLogit爆炸现象。回顾Attention的定义
\begin{equation}\boldsymbol{O} = softmax(\boldsymbol{Q}\boldsymbol{K}^{\top})\boldsymbol{V}\end{equation}
Transformer升级之路:21、MLA好在哪里?(下)
By 苏剑林 | 2025-07-10 | 74275位读者 | 引用“对角+低秩”三角阵的高效求逆方法
By 苏剑林 | 2025-07-01 | 28325位读者 | 引用从文章《线性注意力简史:从模仿、创新到反哺》我们可以发现,DeltaNet及其后的线性Attention模型,基本上都关联到了逆矩阵$(\boldsymbol{I} + \boldsymbol{K}\boldsymbol{K}^{\top}\odot\boldsymbol{M}^-)^{-1}$。本文就专门来探讨一下这类具有“对角+低秩”特点的三角矩阵的逆矩阵计算。
基本结果
我们将问题一般地定义如下:
给定矩阵$\boldsymbol{Q},\boldsymbol{K}\in\mathbb{R}^{n\times d}$和对角矩阵$\boldsymbol{\Lambda}\in\mathbb{R}^{n\times n}$,满足$n\gg d$,定义 \begin{equation}\boldsymbol{T} = \boldsymbol{\Lambda} + \boldsymbol{Q}\boldsymbol{K}^{\top}\odot\boldsymbol{M}^-\end{equation} 其中$\boldsymbol{M}^-=\boldsymbol{M} - \boldsymbol{I}$,矩阵$\boldsymbol{M}$定义为 \begin{equation}M_{i,j} = \left\{\begin{aligned} &1, &i \geq j \\ &0, &i < j\end{aligned}\right.\end{equation} 现在要求逆矩阵$\boldsymbol{T}^{-1}$,并且证明其复杂度是$\mathcal{O}(n^2)$。
线性注意力简史:从模仿、创新到反哺
By 苏剑林 | 2025-06-20 | 80005位读者 | 引用在中文圈,本站应该算是比较早关注线性Attention的了,在2020年写首篇相关博客《线性Attention的探索:Attention必须有个Softmax吗?》时,大家主要讨论的还是BERT相关的Softmax Attention。事后来看,在BERT时代考虑线性Attention并不是太明智,因为当时训练长度比较短,且模型主要还是Encoder,用线性Attention来做基本没有优势。对此,笔者也曾撰文《线性Transformer应该不是你要等的那个模型》表达这一观点。
直到ChatGPT的出世,倒逼大家都去做Decoder-only的生成式模型,这跟线性Attention的RNN形式高度契合。同时,追求更长的训练长度也使得Softmax Attention的二次复杂度瓶颈愈发明显。在这样的新背景下,线性Attention越来越体现出竞争力,甚至出现了“反哺”Softmax Attention的迹象。
Transformer升级之路:20、MLA好在哪里?(上)
By 苏剑林 | 2025-05-04 | 88399位读者 | 引用自从DeepSeek爆火后,它所提的Attention变体MLA(Multi-head Latent Attention)也愈发受到关注。MLA通过巧妙的设计实现了MHA与MQA的自由切换,使得模型可以根据训练和推理的不同特性(Compute-Bound or Memory-Bound)选择最佳的形式,尽可能地达到效率最大化。
诚然,MLA很有效,但也有观点认为它不够优雅,所以寻找MLA替代品的努力一直存在,包括我们也有在尝试。然而,经过一段时间的实验,我们发现很多KV Cache相同甚至更大的Attention变体,最终效果都不如MLA。这不得不让我们开始反思:MLA的出色表现背后的关键原因究竟是什么?
接下来,本文将详细介绍笔者围绕这一问题的思考过程以及相关实验结果。
观察
MLA提出自DeepSeek-V2,本文假设读者已经熟悉MLA,至少了解之前的博客《缓存与效果的极限拉扯:从MHA、MQA、GQA到MLA》所介绍的内容,因此MLA自身的细节将不会过多展开。
Transformer升级之路:19、第二类旋转位置编码
By 苏剑林 | 2025-04-18 | 53042位读者 | 引用持续将“Transformer升级之路”系列关注到本篇的读者,想必都已经对旋转位置编码(RoPE)有所了解。简单来说,RoPE是施加在Attention的Query($\boldsymbol{Q}$)和Key($\boldsymbol{K}$)上的旋转变换,形式上属于绝对位置编码,但结合Attention的内积(Dot-Product)特性,能够自动实现相对位置的效果。
那么,RoPE可以加在Value($\boldsymbol{V}$)上吗?看上去不可以,因为对$\boldsymbol{V}$旋转后就不是相对位置编码了。然而事情并没有那么绝对,本文就来讨论加在$\boldsymbol{V}$上RoPE,我们可以称之为“第二类旋转位置编码”。
基础回顾
我们将Dot-Product Attention分解为
\begin{equation}\boldsymbol{o}_i = \sum_j a_{i,j}\boldsymbol{v}_j,\qquad a_{i,j} = \frac{e^{s_{i,j}}}{\sum\limits_j e^{s_{i,j}}},\qquad s_{i,j} = \boldsymbol{q}_i^{\top}\boldsymbol{k}_j\end{equation}








最近评论