用RecomposIt简单给图片换背景
By 苏剑林 | 2010-04-24 | 33951位读者 | Kimi 引用4月21日全国哀悼日,科学空间深切哀悼
By 苏剑林 | 2010-04-20 | 18689位读者 | Kimi 引用【奥赛之行】非同一般的天文奥赛
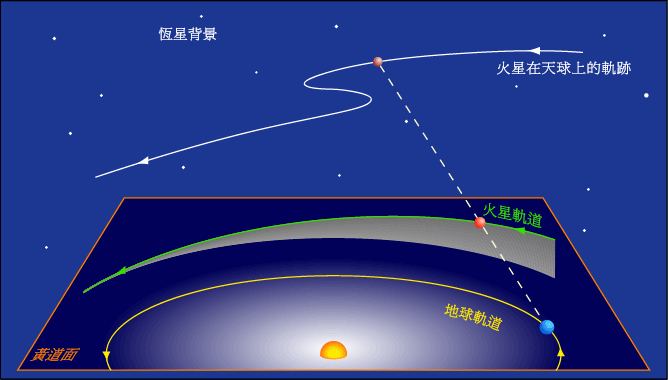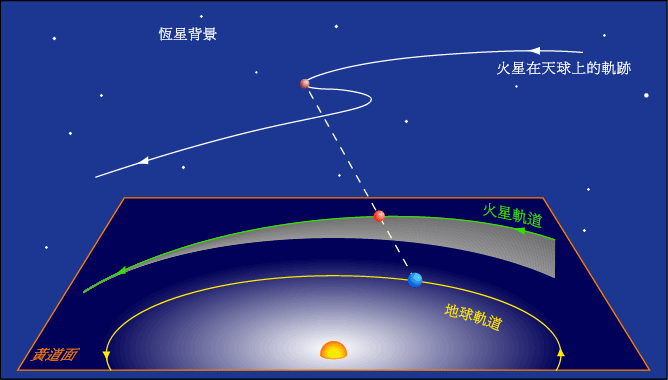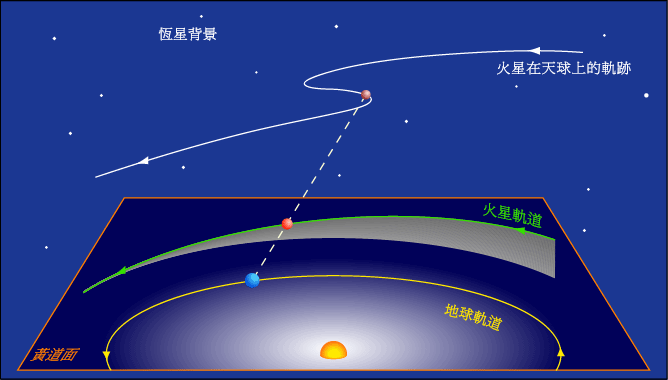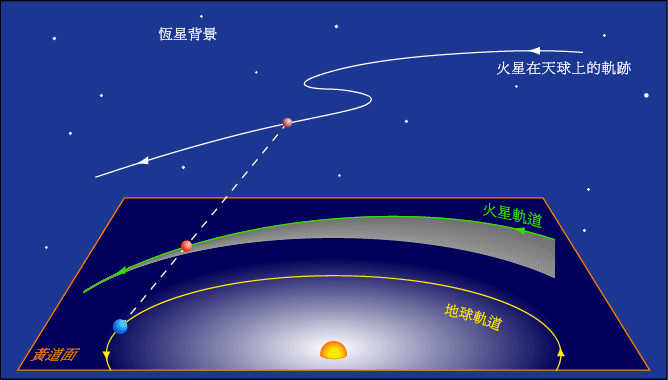
By 苏剑林 | 2010-04-18 | 27980位读者 | Kimi 引用行星的逆行,顺行和留(计算公式)
By 苏剑林 | 2010-04-18 | 81179位读者 | Kimi 引用Lamost被冠名为“郭守敬望远镜”
By 苏剑林 | 2010-04-17 | 64858位读者 | Kimi 引用2010年4月全球天文月(One People,One Sky)
By 苏剑林 | 2010-04-06 | 101356位读者 | Kimi 引用【生物总结】到细胞内旅游
By 苏剑林 | 2010-04-05 | 33037位读者 | Kimi 引用数值方法解方程之终极算法
By 苏剑林 | 2010-04-04 | 60018位读者 | Kimi 引用呵呵,做了一回标题党,可能说得夸张了一点。说是“终极算法”,主要是因为它可以任意提高精度、而且几乎可以应付任何非线性方程(至少理论上是这样),提高精度是已知的迭代式上添加一些项,而不是完全改变迭代式的形式,当然在提高精度的同时,计算量也会随之增大。其理论基础依旧是泰勒级数。
我们考虑方程$x=f(y)$,已知y求x是很容易的,但是已知x求y并不容易。我们考虑把y在$(x_0,y_0)$处展开成x的的泰勒级数。关键是求出y的n阶导数$\frac{d^n y}{dx^n}$。我们记$f^{(n)}(y)=\frac{d^n x}{dy^n}$,并且有
$$\frac{dy}{dx}=\frac{1}{(\frac{dx}{dy})}=f'(y)^{-1}$$







 感谢国家天文台LAMOST项目之“宇宙驿站”提供网络空间和数据库资源! 感谢国家天文台崔辰州博士等人的多方努力和技术支持!
感谢国家天文台LAMOST项目之“宇宙驿站”提供网络空间和数据库资源! 感谢国家天文台崔辰州博士等人的多方努力和技术支持! 科学空间致力于知识分享,所以欢迎您转载本站文章,但转载本站内容必须遵循 署名-非商业用途-保持一致 的创作共用协议。
科学空间致力于知识分享,所以欢迎您转载本站文章,但转载本站内容必须遵循 署名-非商业用途-保持一致 的创作共用协议。 





最近评论