Transformer升级之路：2、博采众长的旋转式位置编码

上一篇文章中，我们对原始的Sinusoidal位置编码做了较为详细的推导和理解，总的感觉是Sinusoidal位置编码是一种“想要成为相对位置编码的绝对位置编码”。一般来说，绝对位置编码具有实现简单、计算速度快等优点，而相对位置编码则直接地体现了相对位置信号，跟我们的直观理解吻合，实际性能往往也更好。由此可见，如果可以通过绝对位置编码的方式实现相对位置编码，那么就是“集各家之所长”、“鱼与熊掌兼得”了。Sinusoidal位置编码隐约做到了这一点，但并不够好。

本文将会介绍我们自研的Rotary Transformer（RoFormer）模型，它的主要改动是应用了笔者构思的“旋转式位置编码（Rotary Position Embedding，RoPE）”，这是一种配合Attention机制能达到“绝对位置编码的方式实现相对位置编码”的设计。而也正因为这种设计，它还是目前唯一一种可用于线性Attention的相对位置编码。

RoFormer：https://github.com/ZhuiyiTechnology/roformer

基本思路 #

在之前的文章《让研究人员绞尽脑汁的Transformer位置编码》中我们就简要介绍过RoPE，当时称之为“融合式”，本文则更加详细地介绍它的来源与性质。在RoPE中，我们的出发点就是“通过绝对位置编码的方式实现相对位置编码”，这样做既有理论上的优雅之处，也有实践上的实用之处，比如它可以拓展到线性Attention中就是主要因为这一点。

为了达到这个目的，我们假设通过下述运算来给$\boldsymbol{q},\boldsymbol{k}$添加绝对位置信息：
\begin{equation}\tilde{\boldsymbol{q}}_m = \boldsymbol{f}(\boldsymbol{q}, m), \quad\tilde{\boldsymbol{k}}_n = \boldsymbol{f}(\boldsymbol{k}, n)\end{equation}
也就是说，我们分别为$\boldsymbol{q},\boldsymbol{k}$设计操作$\boldsymbol{f}(\cdot, m),\boldsymbol{f}(\cdot, n)$，使得经过该操作后，$\tilde{\boldsymbol{q}}_m,\tilde{\boldsymbol{k}}_n$就带有了位置$m,n$的绝对位置信息。Attention的核心运算是内积，所以我们希望的内积的结果带有相对位置信息，因此假设存在恒等关系：
\begin{equation}\langle\boldsymbol{f}(\boldsymbol{q}, m), \boldsymbol{f}(\boldsymbol{k}, n)\rangle = g(\boldsymbol{q},\boldsymbol{k},m-n)\end{equation}
所以我们要求出该恒等式的一个（尽可能简单的）解。求解过程还需要一些初始条件，显然我们可以合理地设$\boldsymbol{f}(\boldsymbol{q}, 0)=\boldsymbol{q}$和$\boldsymbol{f}(\boldsymbol{k}, 0)=\boldsymbol{k}$。

求解过程 #

同上一篇思路一样，我们先考虑二维情形，然后借助复数来求解。在复数中有$\langle\boldsymbol{q},\boldsymbol{k}\rangle=\text{Re}[\boldsymbol{q}\boldsymbol{k}^*]$，$\text{Re}[]$代表复数的实部，所以我们有
\begin{equation}\text{Re}[\boldsymbol{f}(\boldsymbol{q}, m)\boldsymbol{f}^*(\boldsymbol{k}, n)] = g(\boldsymbol{q},\boldsymbol{k},m-n)\end{equation}
简单起见，我们假设存在复数$\boldsymbol{g}(\boldsymbol{q},\boldsymbol{k},m-n)$，使得$\boldsymbol{f}(\boldsymbol{q}, m)\boldsymbol{f}^*(\boldsymbol{k}, n) = \boldsymbol{g}(\boldsymbol{q},\boldsymbol{k},m-n)$，然后我们用复数的指数形式，设
\begin{equation}\begin{aligned}
\boldsymbol{f}(\boldsymbol{q}, m) =&\, R_f (\boldsymbol{q}, m)e^{\text{i}\Theta_f(\boldsymbol{q}, m)} \\
\boldsymbol{f}(\boldsymbol{k}, n) =&\, R_f (\boldsymbol{k}, n)e^{\text{i}\Theta_f(\boldsymbol{k}, n)} \\
\boldsymbol{g}(\boldsymbol{q}, \boldsymbol{k}, m-n) =&\, R_g (\boldsymbol{q}, \boldsymbol{k}, m-n)e^{\text{i}\Theta_g(\boldsymbol{q}, \boldsymbol{k}, m-n)} \\
\end{aligned}\end{equation}
那么代入方程后就得到方程组
\begin{equation}\begin{aligned}
R_f (\boldsymbol{q}, m) R_f (\boldsymbol{k}, n) =&\, R_g (\boldsymbol{q}, \boldsymbol{k}, m-n) \\
\Theta_f (\boldsymbol{q}, m) - \Theta_f (\boldsymbol{k}, n) =&\, \Theta_g (\boldsymbol{q}, \boldsymbol{k}, m-n)
\end{aligned}\end{equation}
对于第一个方程，代入$m=n$得到
\begin{equation}R_f (\boldsymbol{q}, m) R_f (\boldsymbol{k}, m) = R_g (\boldsymbol{q}, \boldsymbol{k}, 0) = R_f (\boldsymbol{q}, 0) R_f (\boldsymbol{k}, 0) = \Vert \boldsymbol{q}\Vert \Vert \boldsymbol{k}\Vert\end{equation}
最后一个等号源于初始条件$\boldsymbol{f}(\boldsymbol{q}, 0)=\boldsymbol{q}$和$\boldsymbol{f}(\boldsymbol{k}, 0)=\boldsymbol{k}$。所以现在我们可以很简单地设$R_f (\boldsymbol{q}, m)=\Vert \boldsymbol{q}\Vert, R_f (\boldsymbol{k}, m)=\Vert \boldsymbol{k}\Vert$，即它不依赖于$m$。至于第二个方程，同样代入$m=n$得到
\begin{equation}\Theta_f (\boldsymbol{q}, m) - \Theta_f (\boldsymbol{k}, m) = \Theta_g (\boldsymbol{q}, \boldsymbol{k}, 0) = \Theta_f (\boldsymbol{q}, 0) - \Theta_f (\boldsymbol{k}, 0) = \Theta (\boldsymbol{q}) - \Theta (\boldsymbol{k})\end{equation}
这里的$\Theta (\boldsymbol{q}),\Theta (\boldsymbol{k})$是$\boldsymbol{q},\boldsymbol{k}$本身的幅角，最后一个等号同样源于初始条件。根据上式得到$\Theta_f (\boldsymbol{q}, m) - \Theta (\boldsymbol{q}) = \Theta_f (\boldsymbol{k}, m) - \Theta (\boldsymbol{k})$，所以$\Theta_f (\boldsymbol{q}, m) - \Theta (\boldsymbol{q})$应该是一个只与$m$相关、跟$\boldsymbol{q}$无关的函数，记为$\varphi(m)$，即$\Theta_f (\boldsymbol{q}, m) = \Theta (\boldsymbol{q}) + \varphi(m)$。接着代入$n=m-1$，整理得到
\begin{equation}\varphi(m) - \varphi(m-1) = \Theta_g (\boldsymbol{q}, \boldsymbol{k}, 1) + \Theta (\boldsymbol{k}) - \Theta (\boldsymbol{q})\end{equation}
即$\{\varphi(m)\}$是等差数列，设右端为$\theta$，那么就解得$\varphi(m)=m\theta$。

编码形式 #

综上，我们得到二维情况下用复数表示的RoPE：
\begin{equation}
\boldsymbol{f}(\boldsymbol{q}, m) = R_f (\boldsymbol{q}, m)e^{\text{i}\Theta_f(\boldsymbol{q}, m)}
= \Vert q\Vert e^{\text{i}(\Theta(\boldsymbol{q}) + m\theta)} = \boldsymbol{q} e^{\text{i}m\theta}\end{equation}
根据复数乘法的几何意义，该变换实际上对应着向量的旋转，所以我们称之为“旋转式位置编码”，它还可以写成矩阵形式：
\begin{equation}
\boldsymbol{f}(\boldsymbol{q}, m) =\begin{pmatrix}\cos m\theta & -\sin m\theta\\ \sin m\theta & \cos m\theta\end{pmatrix} \begin{pmatrix}q_0 \\ q_1\end{pmatrix}\end{equation}
由于内积满足线性叠加性，因此任意偶数维的RoPE，我们都可以表示为二维情形的拼接，即
\begin{equation}\scriptsize{\underbrace{\begin{pmatrix}
\cos m\theta_0 & -\sin m\theta_0 & 0 & 0 & \cdots & 0 & 0 \\
\sin m\theta_0 & \cos m\theta_0 & 0 & 0 & \cdots & 0 & 0 \\
0 & 0 & \cos m\theta_1 & -\sin m\theta_1 & \cdots & 0 & 0 \\
0 & 0 & \sin m\theta_1 & \cos m\theta_1 & \cdots & 0 & 0 \\
\vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\
0 & 0 & 0 & 0 & \cdots & \cos m\theta_{d/2-1} & -\sin m\theta_{d/2-1} \\
0 & 0 & 0 & 0 & \cdots & \sin m\theta_{d/2-1} & \cos m\theta_{d/2-1} \\
\end{pmatrix}}_{\boldsymbol{\mathcal{R}}_m} \begin{pmatrix}q_0 \\ q_1 \\ q_2 \\ q_3 \\ \vdots \\ q_{d-2} \\ q_{d-1}\end{pmatrix}}\end{equation}
也就是说，给位置为$m$的向量$\boldsymbol{q}$乘上矩阵$\boldsymbol{\mathcal{R}}_m$、位置为$n$的向量$\boldsymbol{k}$乘上矩阵$\boldsymbol{\mathcal{R}}_n$，用变换后的$\boldsymbol{Q},\boldsymbol{K}$序列做Attention，那么Attention就自动包含相对位置信息了，因为成立恒等式：
\begin{equation}(\boldsymbol{\mathcal{R}}_m \boldsymbol{q})^{\top}(\boldsymbol{\mathcal{R}}_n \boldsymbol{k}) = \boldsymbol{q}^{\top} \boldsymbol{\mathcal{R}}_m^{\top}\boldsymbol{\mathcal{R}}_n \boldsymbol{k} = \boldsymbol{q}^{\top} \boldsymbol{\mathcal{R}}_{n-m} \boldsymbol{k}\end{equation}
值得指出的是，$\boldsymbol{\mathcal{R}}_m$是一个正交矩阵，它不会改变向量的模长，因此通常来说它不会改变原模型的稳定性。

由于$\boldsymbol{\mathcal{R}}_m$的稀疏性，所以直接用矩阵乘法来实现会很浪费算力，推荐通过下述方式来实现RoPE：
\begin{equation}\begin{pmatrix}q_0 \\ q_1 \\ q_2 \\ q_3 \\ \vdots \\ q_{d-2} \\ q_{d-1}
\end{pmatrix}\otimes\begin{pmatrix}\cos m\theta_0 \\ \cos m\theta_0 \\ \cos m\theta_1 \\ \cos m\theta_1 \\ \vdots \\ \cos m\theta_{d/2-1} \\ \cos m\theta_{d/2-1}
\end{pmatrix} + \begin{pmatrix}-q_1 \\ q_0 \\ -q_3 \\ q_2 \\ \vdots \\ -q_{d-1} \\ q_{d-2}
\end{pmatrix}\otimes\begin{pmatrix}\sin m\theta_0 \\ \sin m\theta_0 \\ \sin m\theta_1 \\ \sin m\theta_1 \\ \vdots \\ \sin m\theta_{d/2-1} \\ \sin m\theta_{d/2-1}
\end{pmatrix}\end{equation}
其中$\otimes$是逐位对应相乘，即Numpy、Tensorflow等计算框架中的$*$运算。从这个实现也可以看到，RoPE可以视为是乘性位置编码的变体。

远程衰减 #

可以看到，RoPE形式上和Sinusoidal位置编码有点相似，只不过Sinusoidal位置编码是加性的，而RoPE可以视为乘性的。在$\theta_i$的选择上，我们同样沿用了Sinusoidal位置编码的方案，即$\theta_i = 10000^{-2i/d}$，它可以带来一定的远程衰减性。

具体证明如下：将$\boldsymbol{q},\boldsymbol{k}$两两分组后，它们加上RoPE后的内积可以用复数乘法表示为
\begin{equation}
(\boldsymbol{\mathcal{R}}_m \boldsymbol{q})^{\top}(\boldsymbol{\mathcal{R}}_n \boldsymbol{k}) = \text{Re}\left[\sum_{i=0}^{d/2-1}\boldsymbol{q}_{[2i:2i+1]}\boldsymbol{k}_{[2i:2i+1]}^* e^{\text{i}(m-n)\theta_i}\right]\end{equation}
记$h_i = \boldsymbol{q}_{[2i:2i+1]}\boldsymbol{k}_{[2i:2i+1]}^*, S_j = \sum\limits_{i=0}^{j-1} e^{\text{i}(m-n)\theta_i}$，并约定$h_{d/2}=0,S_0=0$，那么由Abel变换（分部求和法）可以得到：
\begin{equation}\sum_{i=0}^{d/2-1}\boldsymbol{q}_{[2i:2i+1]}\boldsymbol{k}_{[2i:2i+1]}^* e^{\text{i}(m-n)\theta_i} = \sum_{i=0}^{d/2-1} h_i (S_{i
+1} - S_i) = -\sum_{i=0}^{d/2-1} S_{i+1}(h_{i+1} - h_i)\end{equation}
所以
\begin{equation}\begin{aligned}
\left|\sum_{i=0}^{d/2-1}\boldsymbol{q}_{[2i:2i+1]}\boldsymbol{k}_{[2i:2i+1]}^* e^{\text{i}(m-n)\theta_i}\right| =&\, \left|\sum_{i=0}^{d/2-1} S_{i+1}(h_{i+1} - h_i)\right| \\
\leq&\, \sum_{i=0}^{d/2-1} |S_{i+1}| |h_{i+1} - h_i| \\
\leq&\, \left(\max_i |h_{i+1} - h_i|\right)\sum_{i=0}^{d/2-1} |S_{i+1}|
\end{aligned}\end{equation}
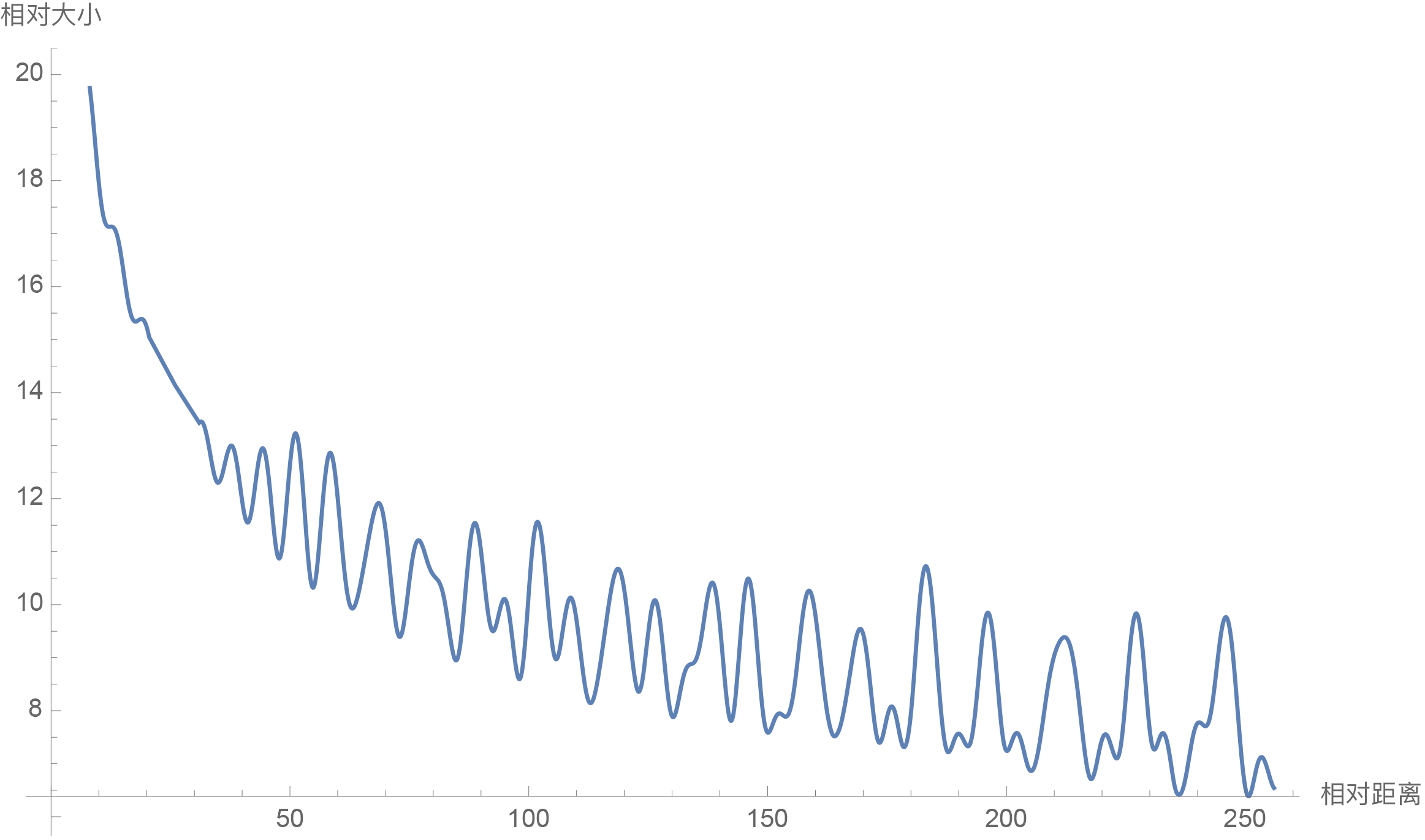
因此我们可以考察$\frac{1}{d/2}\sum\limits_{i=1}^{d/2} |S_i|$随着相对距离的变化情况来作为衰减性的体现，Mathematica代码如下：

d = 128;
\[Theta][t_] = 10000^(-2*t/d);
f[m_] = Sum[
    Norm[Sum[Exp[I*m*\[Theta][i]], {i, 0, j}]], {j, 0, d/2 - 1}]/(d/2);
Plot[f[m], {m, 0, 256}, AxesLabel -> {相对距离, 相对大小}]

结果如下图：

RoPE的远程衰减性（d=128）

从图中我们可以可以看到随着相对距离的变大，内积结果有衰减趋势的出现。因此，选择$\theta_i = 10000^{-2i/d}$，确实能带来一定的远程衰减性。当然，同上一篇文章说的一样，能带来远程衰减性的不止这个选择，几乎任意的光滑单调函数都可以，这里只是沿用了已有的选择而已。笔者还试过以$\theta_i = 10000^{-2i/d}$为初始化，将$\theta_i$视为可训练参数，然后训练一段时间后发现$\theta_i$并没有显著更新，因此干脆就直接固定$\theta_i = 10000^{-2i/d}$了。

线性场景 #

最后，我们指出，RoPE是目前唯一一种可以用于线性Attention的相对位置编码。这是因为其他的相对位置编码，都是直接基于Attention矩阵进行操作的，但是线性Attention并没有事先算出Attention矩阵，因此也就不存在操作Attention矩阵的做法，所以其他的方案无法应用到线性Attention中。而对于RoPE来说，它是用绝对位置编码的方式来实现相对位置编码，不需要操作Attention矩阵，因此有了应用到线性Attention的可能性。

关于线性Attention的介绍，这里不再重复，有需要的读者请参考《线性Attention的探索：Attention必须有个Softmax吗？》。线性Attention的常见形式是：
\begin{equation}Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V})_i = \frac{\sum\limits_{j=1}^n \text{sim}(\boldsymbol{q}_i, \boldsymbol{k}_j)\boldsymbol{v}_j}{\sum\limits_{j=1}^n \text{sim}(\boldsymbol{q}_i, \boldsymbol{k}_j)} = \frac{\sum\limits_{j=1}^n \phi(\boldsymbol{q}_i)^{\top} \varphi(\boldsymbol{k}_j)\boldsymbol{v}_j}{\sum\limits_{j=1}^n \phi(\boldsymbol{q}_i)^{\top} \varphi(\boldsymbol{k}_j)}\end{equation}
其中$\phi,\varphi$是值域非负的激活函数。可以看到，线性Attention也是基于内积的，所以很自然的想法是可以将RoPE插入到内积中：
\begin{equation}\frac{\sum\limits_{j=1}^n [\boldsymbol{\mathcal{R}}_i\phi(\boldsymbol{q}_i)]^{\top} [\boldsymbol{\mathcal{R}}_j\varphi(\boldsymbol{k}_j)]\boldsymbol{v}_j}{\sum\limits_{j=1}^n [\boldsymbol{\mathcal{R}}_i\phi(\boldsymbol{q}_i)]^{\top} [\boldsymbol{\mathcal{R}}_j\varphi(\boldsymbol{k}_j)]}\end{equation}
但这样存在的问题是，内积$[\boldsymbol{\mathcal{R}}_i\phi(\boldsymbol{q}_i)]^{\top} [\boldsymbol{\mathcal{R}}_j\varphi(\boldsymbol{k}_j)]$可能为负数，因此它不再是常规的概率注意力，而且分母有为0的风险，可能会带来优化上的不稳定。考虑到$\boldsymbol{\mathcal{R}}_i,\boldsymbol{\mathcal{R}}_j$都是正交矩阵，它不改变向量的模长，因此我们可以抛弃常规的概率归一化要求，使用如下运算作为一种新的线性Attention：
\begin{equation}\frac{\sum\limits_{j=1}^n [\boldsymbol{\mathcal{R}}_i\phi(\boldsymbol{q}_i)]^{\top} [\boldsymbol{\mathcal{R}}_j\varphi(\boldsymbol{k}_j)]\boldsymbol{v}_j}{\sum\limits_{j=1}^n \phi(\boldsymbol{q}_i)^{\top} \varphi(\boldsymbol{k}_j)}\end{equation}
也就是说，RoPE只插入分子中，而分母则不改变，这样的注意力不再是基于概率的（注意力矩阵不再满足非负归一性），但它某种意义上来说也是一个归一化方案，而且也没有证据表明非概率式的注意力就不好（比如Nyströmformer也算是没有严格依据概率分布的方式构建注意力），所以我们将它作为候选方案之一进行实验，而我们初步的实验结果显示这样的线性Attention也是有效的。

此外，笔者在《线性Attention的探索：Attention必须有个Softmax吗？》中还提出过另外一种线性Attention方案：$\text{sim}(\boldsymbol{q}_i, \boldsymbol{k}_j) = 1 + \left( \frac{\boldsymbol{q}_i}{\Vert \boldsymbol{q}_i\Vert}\right)^{\top}\left(\frac{\boldsymbol{k}_j}{\Vert \boldsymbol{k}_j\Vert}\right)$，它不依赖于值域的非负性，而RoPE也不改变模长，因此RoPE可以直接应用于此类线性Attention，并且不改变它的概率意义。

模型开源 #

RoFormer的第一版模型，我们已经完成训练并开源到了Github中：

RoFormer：https://github.com/ZhuiyiTechnology/roformer

简单来说，RoFormer是一个绝对位置编码替换为RoPE的WoBERT模型，它跟其他模型的结构对比如下：
\begin{array}{c|cccc}
\hline
& \text{BERT} & \text{WoBERT} & \text{NEZHA} & \text{RoFormer} \\
\hline
\text{token单位} & \text{字} & \text{词} & \text{字} & \text{词} & \\
\text{位置编码} & \text{绝对位置} & \text{绝对位置} & \text{经典式相对位置} & \text{RoPE}\\
\hline
\end{array}
在预训练上，我们以WoBERT Plus为基础，采用了多个长度和batch size交替训练的方式，让模型能提前适应不同的训练场景：
\begin{array}{c|ccccc}
\hline
& \text{maxlen} & \text{batch size} & \text{训练步数} & \text{最终loss} & \text{最终acc}\\
\hline
1 & 512 & 256 & 20\text{万} & 1.73 & 65.0\%\\
2 & 1536 & 256 & 1.25\text{万} & 1.61 & 66.8\%\\
3 & 256 & 256 & 12\text{万} & 1.75 & 64.6\%\\
4 & 128 & 512 & 8\text{万} & 1.83 & 63.4\%\\
5 & 1536 & 256 & 1\text{万} & 1.58 & 67.4\%\\
6 & 512 & 512 & 3\text{万} & 1.66 & 66.2\%\\
\hline
\end{array}
从表格还可以看到，增大序列长度，预训练的准确率反而有所提升，这侧面体现了RoFormer长文本语义的处理效果，也体现了RoPE具有良好的外推能力。在短文本任务上，RoFormer与WoBERT的表现类似，RoFormer的主要特点是可以直接处理任意长的文本。下面是我们在CAIL2019-SCM任务上的实验结果：
\begin{array}{c|cc}
\hline
& \text{验证集} & \text{测试集} \\
\hline
\text{BERT-512} & 64.13\% & 67.77\% \\
\text{WoBERT-512} & 64.07\% & 68.10\% \\
\text{RoFormer-512} & 64.13\% & 68.29\% \\
\text{RoFormer-1024} & \textbf{66.07%} & \textbf{69.79%} \\
\hline
\end{array}
其中$\text{-}$后面的参数是微调时截断的maxlen，可以看到RoFormer确实能较好地处理长文本语义，至于设备要求，在24G显存的卡上跑maxlen=1024，batch_size可以跑到8以上。目前中文任务中笔者也就找到这个任务比较适合作为长文本能力的测试，所以长文本方面只测了这个任务，欢迎读者进行测试或推荐其他评测任务。

当然，尽管理论上RoFormer能处理任意长度的序列，但目前RoFormer还是具有平方复杂度的，我们也正在训练基于线性Attention的RoFormer模型，实验完成后也会开源放出，请大家期待。

（注：RoPE和RoFormer已经整理成文《RoFormer: Enhanced Transformer with Rotary Position Embedding》提交到了Arxiv，欢迎使用和引用哈哈～）

文章小结 #

本文介绍了我们自研的旋转式位置编码RoPE以及对应的预训练模型RoFormer。从理论上来看，RoPE与Sinusoidal位置编码有些相通之处，但RoPE不依赖于泰勒展开，更具严谨性与可解释性；从预训练模型RoFormer的结果来看，RoPE具有良好的外推性，应用到Transformer中体现出较好的处理长文本的能力。此外，RoPE还是目前唯一一种可用于线性Attention的相对位置编码。

转载到请包括本文地址：https://www.kexue.fm/archives/8265

更详细的转载事宜请参考：《科学空间FAQ》

打赏

微信打赏

支付宝打赏

因为网站后台对打赏并无记录，因此欢迎在打赏时候备注留言。
你还可以点击这里或在下方评论区留言来告知你的建议或需求。