Performer:用随机投影将Attention的复杂度线性化
By 苏剑林 | 2020-12-01 | 115588位读者 |Attention机制的$\mathcal{O}(n^2)$复杂度是一个老大难问题了,改变这一复杂度的思路主要有两种:一是走稀疏化的思路,比如我们以往介绍过的Sparse Attention以及Google前几个月搞出来的Big Bird,等等;二是走线性化的思路,这部分工作我们之前总结在《线性Attention的探索:Attention必须有个Softmax吗?》中,读者可以翻看一下。本文则介绍一项新的改进工作Performer,出自Google的文章《Rethinking Attention with Performers》,它的目标相当霸气:通过随机投影,在不损失精度的情况下,将Attention的复杂度线性化。
说直接点,就是理想情况下我们可以不用重新训练模型,输出结果也不会有明显变化,但是复杂度降到了$\mathcal{O}(n)$!看起来真的是“天上掉馅饼”般的改进了,真的有这么美好吗?
Attention #
我们知道,Attention的一般定义为:
\begin{equation}Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V})_i = \frac{\sum\limits_{j=1}^n \text{sim}(\boldsymbol{q}_i, \boldsymbol{k}_j)\boldsymbol{v}_j}{\sum\limits_{j=1}^n \text{sim}(\boldsymbol{q}_i, \boldsymbol{k}_j)}\label{eq:gen-att}\end{equation}
对于标准的Scaled-Dot Attention来说,$\text{sim}(\boldsymbol{q}, \boldsymbol{k})=e^{\boldsymbol{q}\cdot \boldsymbol{k}}$(有时候指数部分还会多个缩放因子,这里我们就不显式写出来了),将整个序列的运算写成矩阵形式就是:
\begin{equation}Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}) = softmax\left(\boldsymbol{Q}\boldsymbol{K}^{\top}\right)\boldsymbol{V}\end{equation}
我们主要关心Self Attention场景,所以一般有$\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V}\in\mathbb{R}^{n\times d}$。在上式中,$\boldsymbol{Q}\boldsymbol{K}^{\top}$这一步相当于要对$n^2$个向量对做内积,得到$n^2$个实数,因此不管时间还是空间复杂度都是$\mathcal{O}(n^2)$的。
而对于线性Attention来说,$\text{sim}(\boldsymbol{q}, \boldsymbol{k})=\phi(\boldsymbol{q})\cdot \varphi(\boldsymbol{k})$,其中$\phi,\varphi$是值域非负的激活函数。这样一来,Attention的核心计算量(式$\eqref{eq:gen-att}$中的分子部分)就变成了
\begin{equation}\left(\phi(\boldsymbol{Q})\varphi(\boldsymbol{K})^{\top}\right)\boldsymbol{V}=\phi(\boldsymbol{Q})\left(\varphi(\boldsymbol{K})^{\top}\boldsymbol{V}\right)\end{equation}
上式左端的复杂度依然是$\mathcal{O}(n^2)$的,由于矩阵乘法满足结合律,我们可以先算后面两个矩阵的乘法,这样复杂度就可以降为$\mathcal{O}(n)$了,详细介绍还是请读者翻看之前的文章《线性Attention的探索:Attention必须有个Softmax吗?》,这里就不过多展开了。
Performer #
现在我们就可以进入到Performer的介绍了,开头已经说了,Performer的出发点还是标准的Attention,所以在它那里还是有$\text{sim}(\boldsymbol{q}, \boldsymbol{k})=e^{\boldsymbol{q}\cdot \boldsymbol{k}}$,然后它希望将复杂度线性化,那就是需要找到新的$\tilde{\boldsymbol{q}}, \tilde{\boldsymbol{k}}$,使得:
\begin{equation}\text{sim}(\boldsymbol{q}, \boldsymbol{k}) \approx \tilde{\boldsymbol{q}}\cdot\tilde{\boldsymbol{k}}\end{equation}
如果找到合理的从$\boldsymbol{q},\boldsymbol{k}$到$\tilde{\boldsymbol{q}},\tilde{\boldsymbol{k}}$的映射方案,便是该思路的最大难度了。
漂亮的随机映射 #
Performer的最大贡献就在于,它找到了一个非常漂亮的映射方案:
\begin{equation}\begin{aligned}
e^{\boldsymbol{q}\cdot \boldsymbol{k}}&=\mathbb{E}_{\boldsymbol{\omega}\sim \mathcal{N}(\boldsymbol{\omega};0,\boldsymbol{1}_d)}\left[e^{\boldsymbol{\omega}\cdot \boldsymbol{q}-\Vert \boldsymbol{q}\Vert^2 / 2} \times e^{\boldsymbol{\omega}\cdot \boldsymbol{k}-\Vert \boldsymbol{k}\Vert^2 / 2}\right]\\[6pt]
&\approx\underbrace{\frac{1}{\sqrt{m}}\begin{pmatrix}e^{\boldsymbol{\omega}_1\cdot \boldsymbol{q}-\Vert \boldsymbol{q}\Vert^2 / 2} \\
e^{\boldsymbol{\omega}_2\cdot \boldsymbol{q}-\Vert \boldsymbol{q}\Vert^2 / 2}\\
\vdots\\
e^{\boldsymbol{\omega}_m\cdot \boldsymbol{q}-\Vert \boldsymbol{q}\Vert^2 / 2} \end{pmatrix}}_{\tilde{\boldsymbol{q}}}
\cdot \underbrace{\frac{1}{\sqrt{m}}\begin{pmatrix}e^{\boldsymbol{\omega}_1\cdot \boldsymbol{k}-\Vert \boldsymbol{k}\Vert^2 / 2} \\
e^{\boldsymbol{\omega}_2\cdot \boldsymbol{k}-\Vert \boldsymbol{k}\Vert^2 / 2}\\
\vdots\\
e^{\boldsymbol{\omega}_m\cdot \boldsymbol{k}-\Vert \boldsymbol{k}\Vert^2 / 2} \end{pmatrix}}_{\tilde{\boldsymbol{k}}}
\end{aligned}\label{eq:core}\end{equation}
我们先分析一下上式究竟说了什么。第一个等号意味着左右两端是恒等的,那也就意味着,只要我们从标准正态分布$\mathcal{N}(\boldsymbol{\omega};0,\boldsymbol{1}_d)$中采样无穷无尽的$\boldsymbol{\omega}$,然后算出$e^{\boldsymbol{\omega}\cdot \boldsymbol{q}-\Vert \boldsymbol{q}\Vert^2 / 2} \times e^{\boldsymbol{\omega}\cdot \boldsymbol{k}-\Vert \boldsymbol{k}\Vert^2 / 2}$的平均,结果就等于$e^{\boldsymbol{q}\cdot \boldsymbol{k}}$,写成积分形式就是:
\begin{equation}\begin{aligned}
&\frac{1}{(2\pi)^{d/2}}\int e^{-\Vert\boldsymbol{\omega}\Vert^2 / 2}\times e^{\boldsymbol{\omega}\cdot \boldsymbol{q}-\Vert \boldsymbol{q}\Vert^2 / 2} \times e^{\boldsymbol{\omega}\cdot \boldsymbol{k}-\Vert \boldsymbol{k}\Vert^2 / 2}d\boldsymbol{\omega}
\\
=&\frac{1}{(2\pi)^{d/2}}\int e^{-\Vert\boldsymbol{\omega}-\boldsymbol{q}-\boldsymbol{k}\Vert^2 / 2 + \boldsymbol{q}\cdot \boldsymbol{k}}d\boldsymbol{\omega}\\
=&\, e^{\boldsymbol{q}\cdot \boldsymbol{k}}
\end{aligned}\end{equation}
当然实际情况下我们只能采样有限的$m$个,因此就得到了第二个约等号,它正好可以表示为两个$m$维向量的内积的形式,这正是我们需要的$e^{\boldsymbol{q}\cdot \boldsymbol{k}}\approx \tilde{\boldsymbol{q}}\cdot\tilde{\boldsymbol{k}}$!所以,借助这个近似,我们就可以将两个$d$维向量的内积的指数,转化为了两个$m$维向量的内积了,从而理论上来说,我们就可以将原来head_size为$d$的标准Attention,转化为head_size为$m$的线性Attention了,这便是整篇论文的核心思路。
推导过程讨论 #
可能有些读者会比较关心式$\eqref{eq:core}$的来源,这里展开讨论一下,当然如果不关心的读者可以直接跳过这一节。尽管直接通过计算积分可以验证式$\eqref{eq:core}$是成立的,但对于任意定义的$\text{sim}(\boldsymbol{q}, \boldsymbol{k})$,是否可以找到类似的线性近似?下面我们将会证明,类似的线性化方案可以通过一个一般化的流程找到,只不过得到的结果可能远远不如式$\eqref{eq:core}$漂亮有效。
具体来说,对于任意的$\text{sim}(\boldsymbol{q}, \boldsymbol{k})$,我们可以改写为
\begin{equation}\text{sim}(\boldsymbol{q}, \boldsymbol{k}) = \frac{\beta(\boldsymbol{q})\gamma(\boldsymbol{k})\text{sim}(\boldsymbol{q}, \boldsymbol{k})}{\beta(\boldsymbol{q})\gamma(\boldsymbol{k})}\end{equation}
然后我们可以对$\beta(\boldsymbol{q})\gamma(\boldsymbol{k})\text{sim}(\boldsymbol{q}, \boldsymbol{k})$做傅里叶变换:
\begin{equation}\mathcal{F}(\boldsymbol{\omega}_q, \boldsymbol{\omega}_k)=\frac{1}{(2\pi)^{d/2}}\int \beta(\boldsymbol{q})\gamma(\boldsymbol{k})\text{sim}(\boldsymbol{q}, \boldsymbol{k})e^{-i\boldsymbol{\omega}_q\cdot \boldsymbol{q}-i\boldsymbol{\omega}_k\cdot \boldsymbol{k}}d\boldsymbol{q}d\boldsymbol{k}\end{equation}
至于为什么要先乘以$\beta(\boldsymbol{q})\gamma(\boldsymbol{k})$,那是因为直接对$\text{sim}(\boldsymbol{q}, \boldsymbol{k})$做傅里叶变换的结果可能不好看甚至不存在,乘一个函数之后可能就可以了,比如可以让$\beta(\boldsymbol{x})=\gamma(\boldsymbol{x})=e^{-\lambda\Vert x\Vert^2}$,只要$\lambda$足够大,就可以让很多$\text{sim}(\boldsymbol{q}, \boldsymbol{k})$都完成傅里叶变换了。
接着我们执行逆变换,并代回原式,就得到
\begin{equation}\text{sim}(\boldsymbol{q}, \boldsymbol{k})=\frac{1}{(2\pi)^{d/2}}\int \mathcal{F}(\boldsymbol{\omega}_q, \boldsymbol{\omega}_k)\frac{e^{i\boldsymbol{\omega}_q\cdot \boldsymbol{q}}}{\beta(\boldsymbol{q})} \frac{e^{i\boldsymbol{\omega}_k\cdot \boldsymbol{k}}}{\gamma(\boldsymbol{k})}d\boldsymbol{\omega}_q d\boldsymbol{\omega}_k\end{equation}
如果我们能算出$\mathcal{F}(\boldsymbol{\omega}_q, \boldsymbol{\omega}_k)$并完成归一化,那么它就可以成为一个可以从中采样的分布,从中可以采样出随机向量$\boldsymbol{\omega}_q,\boldsymbol{\omega}_k$来,然后近似转化为$\frac{e^{i\boldsymbol{\omega}_q\cdot \boldsymbol{q}}}{\beta(\boldsymbol{q})}, \frac{e^{i\boldsymbol{\omega}_k\cdot \boldsymbol{k}}}{\gamma(\boldsymbol{k})}$组成的向量序列的内积。当然,这里的运算可能涉及到虚数,而我们一般只是处理实数,但这问题不大,我们可以用欧拉公式$e^{i \theta}=\cos\theta + i\sin\theta$展开,整个运算过程只保留实部即可,形式不会有太大的变化。理论上来说,整套流程可以走下来,不会有什么困难,但是相比式$\eqref{eq:core}$,存在的问题是:1、现在需要采样两组随机变量$\boldsymbol{\omega}_q,\boldsymbol{\omega}_k$,会扩大估计的方差;2、最终保留实部后,得到的将会是$\sin,\cos$的组合形式,其结果无法保证非负性,需要额外的clip来处理。
而式$\eqref{eq:core}$的特别之处在于,$e^{\boldsymbol{q}\cdot \boldsymbol{k}}$可以改写为
\begin{equation}e^{\boldsymbol{q}\cdot \boldsymbol{k}} = e^{\Vert \boldsymbol{q}\Vert^2 / 2 + \Vert \boldsymbol{k}\Vert^2 / 2 - \Vert\boldsymbol{q}-\boldsymbol{k}\Vert^2 / 2}\end{equation}
所以只需要转化为单个变量$\boldsymbol{q}-\boldsymbol{k}$的问题,而$e^{-\Vert\boldsymbol{q}-\boldsymbol{k}\Vert^2 / 2}$的傅里叶变换正好是$e^{-\Vert\boldsymbol{\omega}\Vert^2 / 2}$,所以做逆变换我们有
\begin{equation}e^{\boldsymbol{q}\cdot \boldsymbol{k}}=\frac{e^{\Vert \boldsymbol{q}\Vert^2 / 2 + \Vert \boldsymbol{k}\Vert^2 / 2}}{(2\pi)^{d/2}}\int e^{-\Vert\boldsymbol{\omega}\Vert^2 / 2 + i \boldsymbol{\omega}\cdot (\boldsymbol{q} - \boldsymbol{k})} d\boldsymbol{\omega}\end{equation}
到这里,如果直接取实部展开,得到的也是$\sin,\cos$的组合,这就是原论文说的$\text{trig}$形式的投影方案。不过,有一个更加巧妙的性质可以改变这一切!注意到上式是一个恒等式,所以我们可以左右两边都置换$\boldsymbol{q}\to -i\boldsymbol{q},\boldsymbol{k}\to i\boldsymbol{k}$,结果是:
\begin{equation}e^{\boldsymbol{q}\cdot \boldsymbol{k}}=\frac{e^{-\Vert \boldsymbol{q}\Vert^2 / 2 - \Vert \boldsymbol{k}\Vert^2 / 2}}{(2\pi)^{d/2}}\int e^{-\Vert\boldsymbol{\omega}\Vert^2 / 2 + \boldsymbol{\omega}\cdot (\boldsymbol{q} + \boldsymbol{k})} d\boldsymbol{\omega}\end{equation}
这便是式$\eqref{eq:core}$。置换$\boldsymbol{q}\to -i\boldsymbol{q},\boldsymbol{k}\to i\boldsymbol{k}$使得上述左边保持不变,并且右边完全脱离虚数还保持了非负性,真的是集众多巧合于一身,“只此一家,别无分号”的感觉~
正交化降低方差 #
除了提出式$\eqref{eq:core}$来对标准Attention进行线性化外,原论文还做了进一步的增强。在式$\eqref{eq:core}$,$\boldsymbol{\omega}_1,\boldsymbol{\omega}_2,\cdots,\boldsymbol{\omega}_m$是独立重复地从$\mathcal{N}(\boldsymbol{\omega};0,\boldsymbol{1}_d)$中采样出来的,而原论文则指出,如果将各个$\boldsymbol{\omega}_i$正交化,能有效地降低估算的方差,提高单次估算的平均精度。
注意,这里的正交化指的是保持$\boldsymbol{\omega}_i$的模长不变,仅仅是对其方向进行施密特正交化。这个操作首先提出在同样是Google的论文《The Unreasonable Effectiveness of Structured Random Orthogonal Embeddings》中,而Performer在其论文附录里边,足足花了6页纸来论证这个事情。这里照搬6页证明显然是不适合的,那对于我们来说,该怎么去理解这个策略比较好呢?
其实,这个策略有效的最根本原因,是采样分布$\mathcal{N}(\boldsymbol{\omega};0,\boldsymbol{1}_d)$的各向同性,即其概率密度函数$(2\pi)^{-d/2}e^{-\Vert\boldsymbol{\omega}\Vert^2 / 2}$只依赖于$\boldsymbol{\omega}$的模长$\Vert\boldsymbol{\omega}\Vert$,所以它在方向上是均匀的。而如果我们要降低估算的方差,那么就应该要降低采样的随机性,使得采样的结果更为均匀一些。而各个向量正交化,是方向上均匀的一种实现方式,换句话说,将各个$\boldsymbol{\omega}_i$正交化促进了采样结果的均匀化,从而降低估算的方差。此外,正交化操作一般只对$m\leq d$有效,如果$m > d$,原论文的处理方式是每$d$个向量为一组分别进行正交化。
我们可以联想到,正交化操作只是让采样的方向更加均匀化,如果要做得更加彻底些,可以让采样的模长也均匀化。具体来说,将标准正态分布变换为$d$维球坐标得到其概率微元为:
\begin{equation}\frac{1}{(2\pi)^{d/2}} r^{d-1} e^{-r^2 /2} dr dS\end{equation}
其中$dS = \sin^{d-2}\varphi_{1} \sin^{d-3}\varphi_{2} \cdots \sin\varphi_{d-2}\,d\varphi_{1}\,d\varphi_{2}\cdots d\varphi_{d-1}$代表在$d$维球面上的积分微元。上式就显示出,标准正态分布在方向是均匀的,模长的概率密度函数正比于$r^{d-1} e^{-r^2 /2}$,我们定义它的累积概率函数:
\begin{equation}P_d(r\leq R) = \frac{\int_0^R r^{d-1} e^{-r^2 /2} dr}{\int_0^{\infty} r^{d-1} e^{-r^2 /2} dr}\end{equation}
如果要采样$m$个样本,那么让$P_d(r\leq R_i) = \frac{i}{m+1},\,i=1,2,\cdots,m$,从中解出$m$个$R_i$作为模长就行了。
性能与效果 #
理论的介绍就到这里了,其实已经展开得都多了,一般来说只要对线性Attention有所了解的话,那么只要看到式$\eqref{eq:core}$,就能很快理解Performer的要点了,剩下的都是锦上添花的内容,不影响全文的主线。接下来我们就主要看对Performer的评测。
原论文的评测 #
我们先来看看原论文的评测,其实它的评测还是很丰富的,但是有点乱,对于主要关心NLP的读者来说可能还有点莫名其妙。
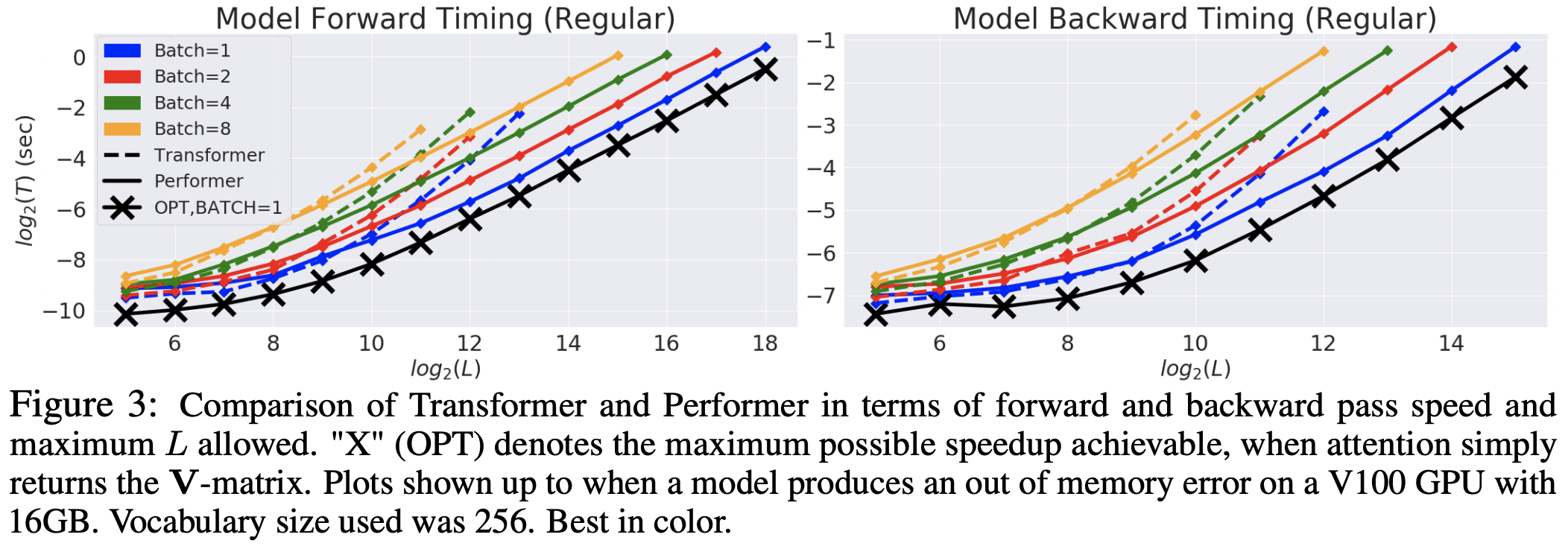
一开始是速度上的评测,这个不意外,反正就是序列长了之后Performer比标准的Transformer有明显优势:
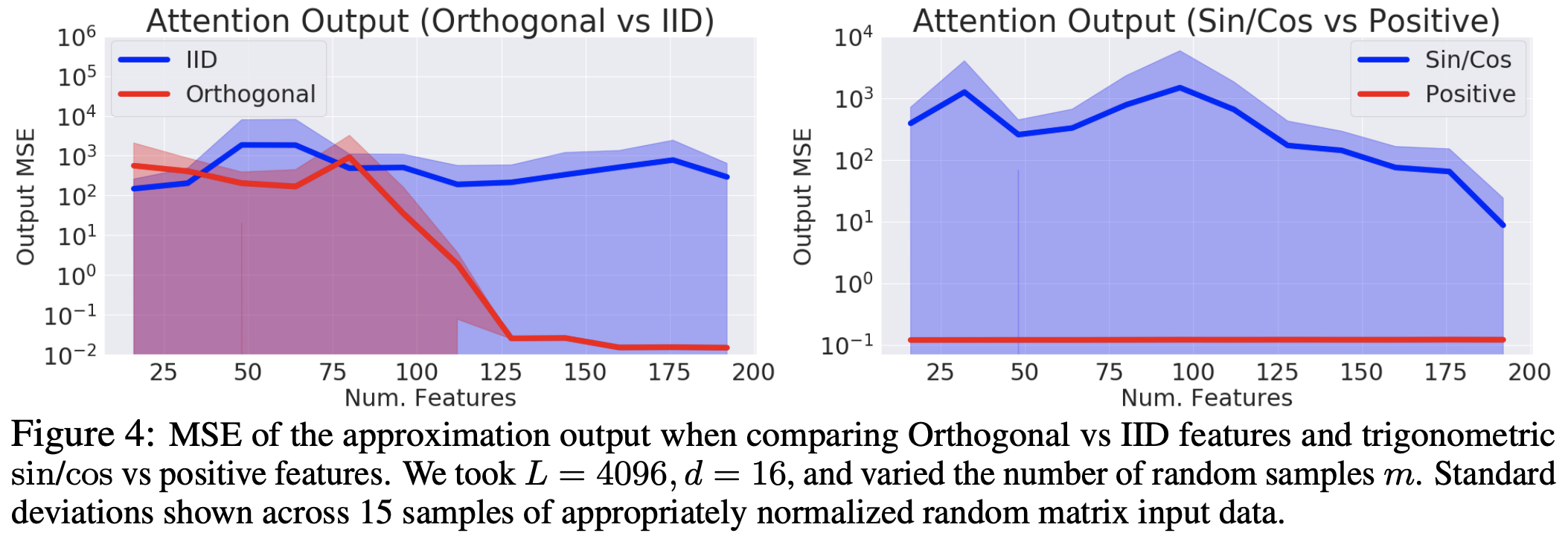
接着,是近似程度的比较,说明了采样正交化的有效性,以及所提的式$\eqref{eq:core}$相比旧的基于$\sin,\cos$函数的形式的精确性:
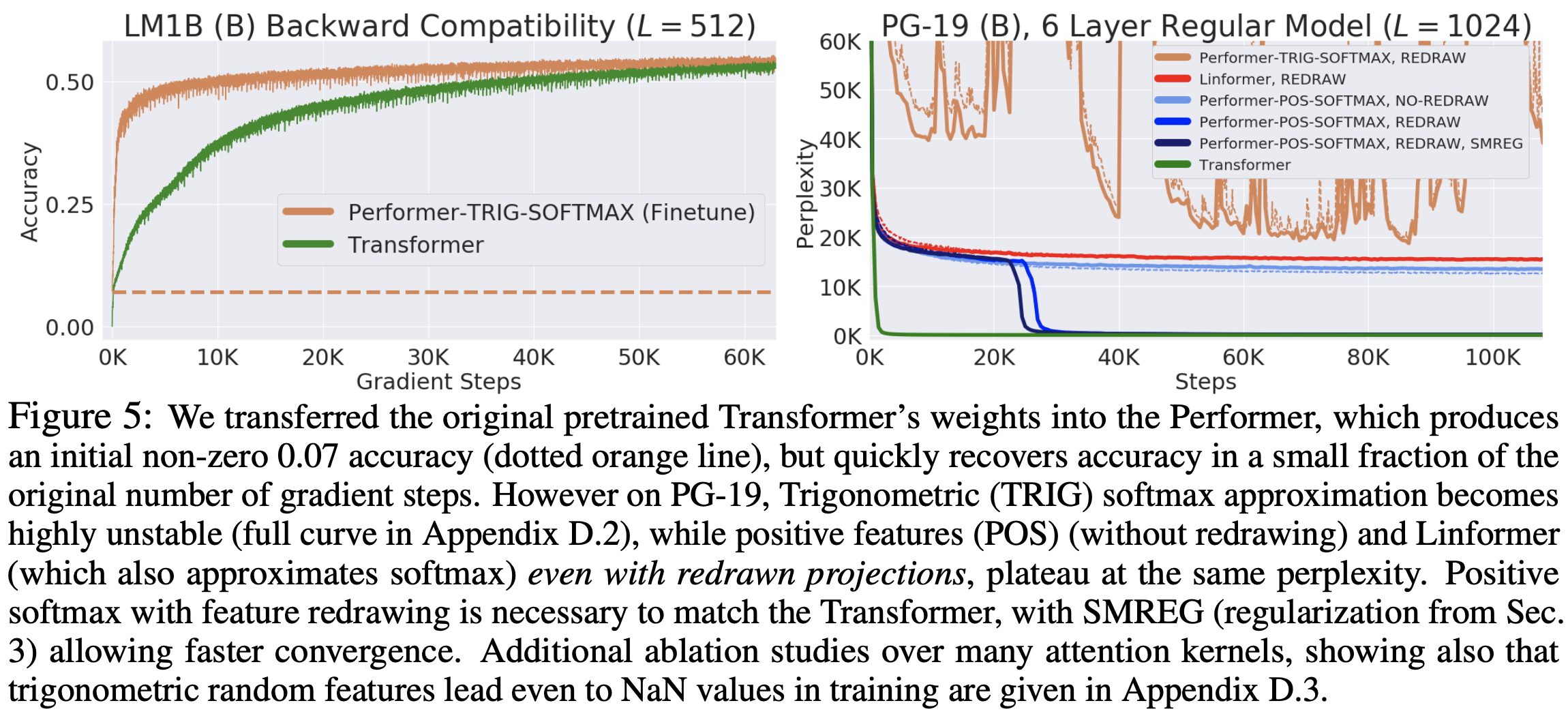
那能不能达到我们一开始的预期目标——不用重新训练已训练好的模型呢?很遗憾,不行,原论文做了两个实验,显示Performer直接加载Transformer的权重不能重现已有的结果,但经过finetune后可以迅速恢复。至于为什么一开始没有很好地重现,论文没有做展开分析。
最后,论文还做了蛋白质序列和图像的实验,证明Performer对于长序列是很有效的,特别地,至少比Reformer有效,全文的实验差不多就是这样,内容很多,但有点找不到北的感觉。
其他论文的评测 #
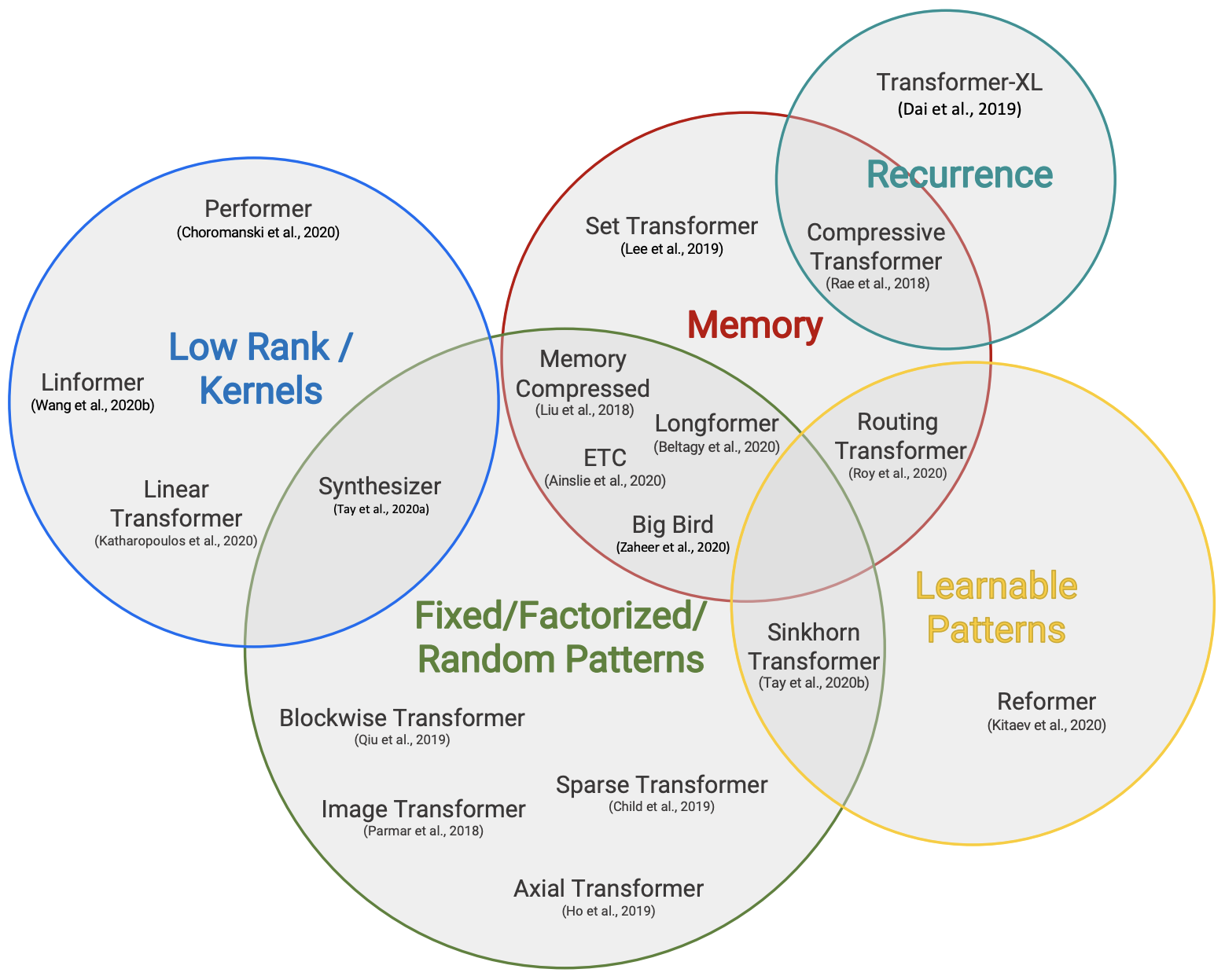
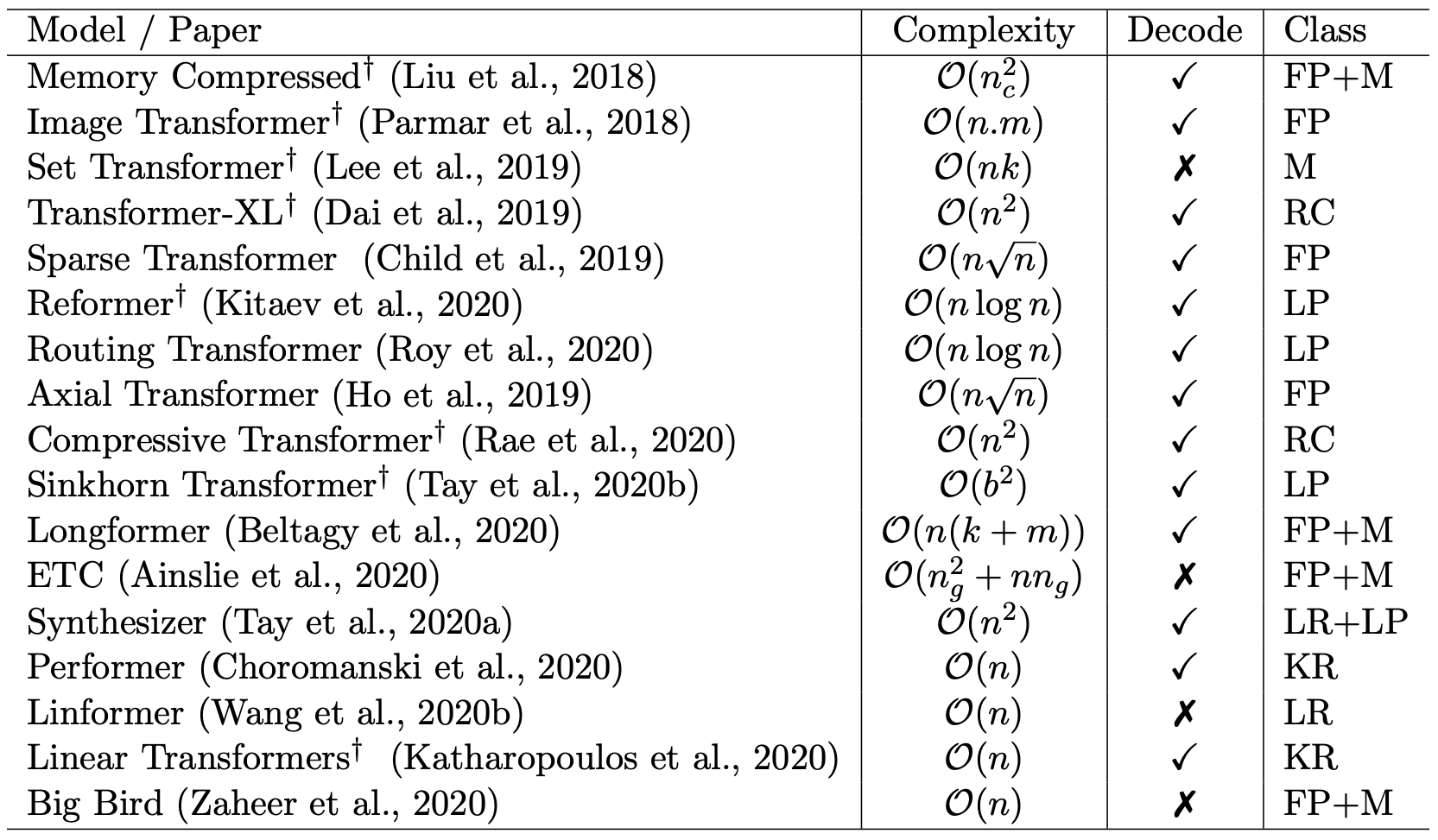
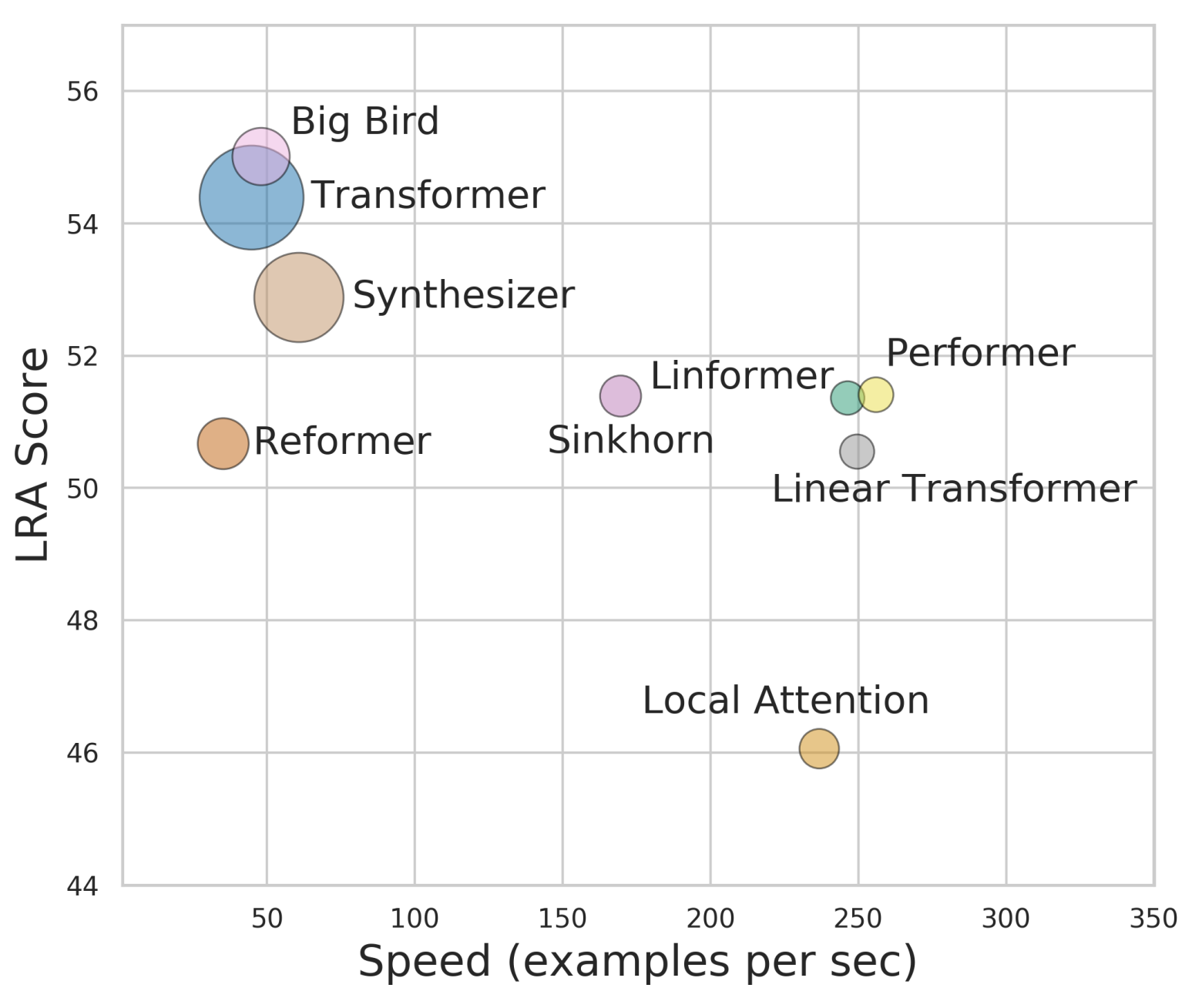
也许是自己的同事都看不下去了,后来Google又出了两篇论文《Efficient Transformers: A Survey》和《Long Range Arena: A Benchmark for Efficient Transformers》,系统地评测和比较了已有的一些改进Transformer效率的方法,其中就包含了Performer。相比之下,这两篇论文给出的结果就直观多了,简单几个图表,就把各个模型的位置给表达清楚了。
更详细的评测信息,大家自行去看这两篇论文就好。
问题与思考 #
看起来Performer是挺不错的,那是不是说我们就可以用它来替代Transformer了?并不是,纵然Performer有诸多可取之处,但仍然存在一些无法解决的问题。
首先,为了更好地近似标准Transformer,Performer的$m$必须取得比较大,至少是$m > d$,一般是$d$的几倍,这也就是说,Performer的head_size要比标准Transformer要明显大。虽然理论上来说,不管$m$多大,只要它固定了,那么Performer关于序列长度的复杂度是线性的,但是$m$变大了,在序列长度比较短时计算量是明显增加的。换句话说,短序列用Performer性能应该是下降的,根据笔者的估计,只有序列长度在5000以上,Performer才会有比较明显的优势。
其次,目前看来Performer(包括其他的线性Attention)跟相对位置编码是不兼容的,因为相对位置编码是直接加在Attention矩阵里边的,Performer连Attention矩阵都没有,自然是加不了的。此外,像UniLM这种特殊的Seq2Seq做法也做不到了,不过普通的单向语言模型还是可以做到的。总之,$\mathcal{O}(n^2)$的Attention矩阵实际上也带来了很大的灵活性,而线性Attention放弃了这个Attention矩阵,也就放弃了这种灵活性了。
最后,也是笔者觉得最大的问题,就是Performer的思想是将标准的Attention线性化,所以为什么不干脆直接训练一个线性Attention模型,而是要向标准Attention靠齐呢?从前面的最后一张图来看,Performer并没有比Linear Transformer有大的优势(而且笔者觉得最后一张图的比较可能有问题,Performer效果可能比Linear Transformer要好,但是速度怎么可能还超过了Linear Transformer?Performer也是转化为Linear Transformer的,多了转化这一步,速度怎能更快?),因此Performer的价值就要打上个问号了,毕竟线性Attention的实现容易得多,而且是通用于长序列/短序列,Performer实现起来则麻烦得多,只适用于长序列。
全文的总结 #
本文主要介绍了Google的新模型Performer,这是一个通过随机投影将标准Attention的复杂度线性化的工作,里边有不少值得我们学习的地方,最后汇总了一下各个改进版Transformer的评测结果,以及分享了笔者对Performer的思考。
转载到请包括本文地址:https://www.kexue.fm/archives/7921
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Dec. 01, 2020). 《Performer:用随机投影将Attention的复杂度线性化 》[Blog post]. Retrieved from https://www.kexue.fm/archives/7921
@online{kexuefm-7921,
title={Performer:用随机投影将Attention的复杂度线性化},
author={苏剑林},
year={2020},
month={Dec},
url={\url{https://www.kexue.fm/archives/7921}},
}










July 1st, 2024
\begin{equation}\frac{1}{(2\pi)^{d/2}} r^{d-1} e^{-r^2 /2} dr dS\end{equation}这个看不懂,d维好难想象。\begin{equation}请问dS = \sin^{d-2}\varphi_{1} \sin^{d-3}\varphi_{2} \cdots \sin\varphi_{d-2}\,d\varphi_{1}\,d\varphi_{2}\cdots d\varphi_{d-1} \\
r^{d-1}中每个r分别对应
\\ sin\varphi_{1}d\varphi_{1},
\\sin\varphi_{1}\sin\varphi_{2}d\varphi_{1}d\varphi_{2},
\\sin\varphi_{1}\sin\varphi_{2}\sin\varphi_{3}d\varphi_{1}d\varphi_{2}d\varphi_{3},
\\sin\varphi_{1}\sin\varphi_{2}\sin\varphi_{3}...\sin\varphi_{d-1}d\varphi_{1}d\varphi_{2}d\varphi_{3}...d\varphi_{d-1}吗?\end{equation}
网上三维球体积微元是 \begin{equation}dV=r^2*sinφdrdθdφ\end{equation}
你自己补习一下多元微积分的变量代换吧,我这里没法一两行给你解释清楚...
谢谢。《n维空间下两个随机向量的夹角分布》https://spaces.ac.cn/archives/7076 在您空间里文章看到了蛛丝马迹。