神秘的圆——三角形的“六接圆”(添加新方法)

数联天地论坛中的watt5151朋友提出了这样的一个问题：

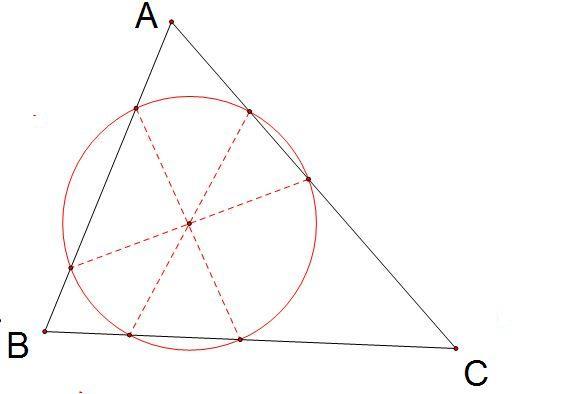
如图，已知三角形ABC，如何做一个圆，它与三角形三边都相交，而且六个交点可以连成三条直径？

三角形的外接圆和内切圆都见多了，看到这样的一个新鲜的题目，BoJone感到很有趣，自作主张地把这个圆称为三角形的“六接圆”，并且在下午研究了一下。最后得出了结论：对于非钝角三角形来说，这和外接圆、内切圆同出一辙，这样的圆总是存在的，而且是唯一存在的；对于钝角三角形， 有些情况是不存在的（虽然可以作出这样的圆，但是与三角形并没有六个交点了，换句话说，圆溢出了）。

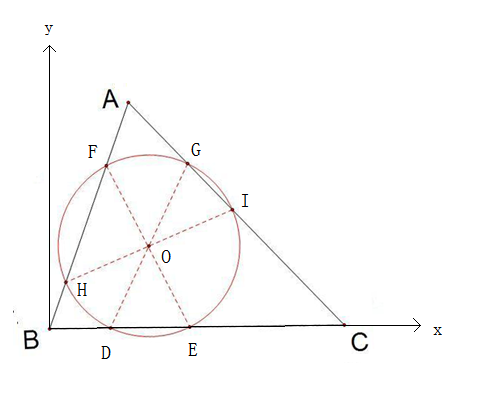
怎么放假一阵子，就感觉好像很久没有做数学题了，头脑都有点生硬了。下面介绍一下BoJone的思考过程，首先作出下图：

设A点的坐标为(a,b)，C点的坐标为(c,0)，并且令所求圆的方程为：$(x-m)^2+(y-n)^2=R^2$。也就是说O点的坐标为(m,n)。不难求出，E、D两点的坐标分别为$(m+-\sqrt{R^2-n^2},0)$。又因为E、O、F三点共线，得到F的坐标为$(m-\sqrt{R^2-n^2},2n)$，同理G的坐标为$(m+\sqrt{R^2-n^2},2n)$。

根据A、F、B三点共线，且AF=BF，可以列出：$$\frac{m-\sqrt{R^2-n^2}}{2n}=\frac{a}{b}\tag{1}$$ 根据A、G、C三点共线，且AG=GC，可以列出：$\frac{m+\sqrt{R^2-n^2}-c}{2n}=\frac{a-c}{b}$——(2)

上面有两条方程，但是有三个未知数m,n,R，剩下一个条件就在于HI这一条直径上，我们可以求出这条直线的方程，然后结合上面两条，把m,n,R确定下来，这说明这个圆是存在且唯一存在的。但是这样处理太麻烦，不方便尺规作图。BoJone按照以下方法处理：

(1)+(2)得出：$\frac{2m-c}{2n}=\frac{2a-c}{b}\Rightarrow 2m-c=\frac{2a-c}{b}(2n)$，这是一道一次函数，过(c/2,0)和(a,b/2)这两点，我们可以方便地在图上把这个函数图像作出来。点O就在这条直线上。

虽然我们现在还不能确定O点在哪儿，但是别忘了，我们现在只是选择了BC边作为x轴，我们还可以选择AB、AC边进行同样的操作，这样可以作出另外一条直线与现有直线相交。由于O点唯一，所以交点必定是O点。知道了O点所在，就等价于知道了m与n的长度（尽管我们不知道具体数据时多少，但是我们也不需要知道，我们只希望能够在图中做出这样的一个圆）。根据(1)式，有$R^2=n^2+(m-\frac{2na}{b})^2$，这是一个尺规可作量。

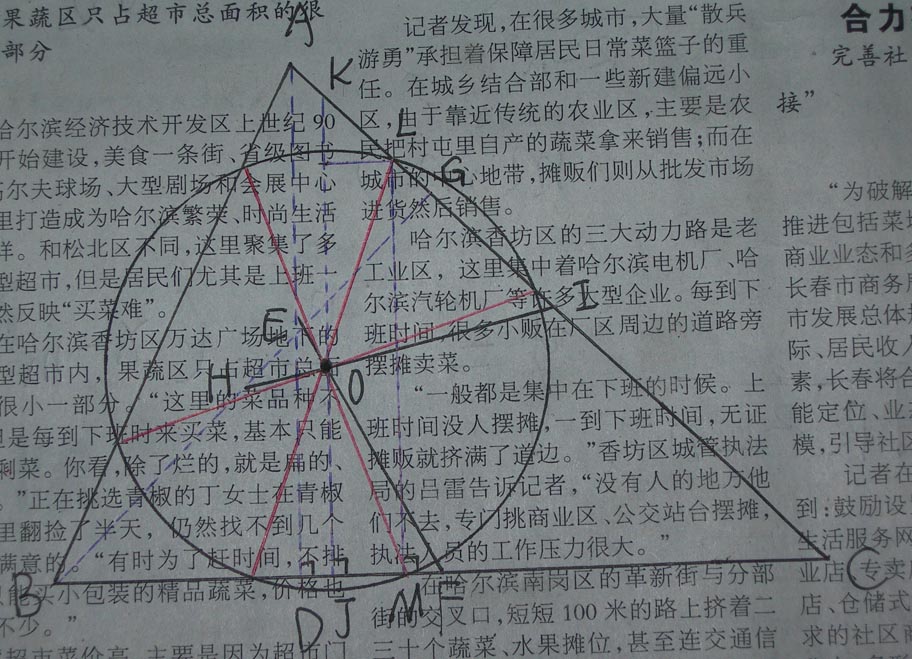
现在我们已经大体研究出了其中的作法，接下来的工作就是把上面的研究“翻译”成尺规作图的步骤。下面是一张BoJone自己在报纸上画的图，用来做一下说明：

步骤：

1、选择三角形的一条边，作出它的中点；并且画出这条边上的高，作出高的中点；
2、作过这两个中点的直线(EF)；
3、选择三角形的另一条边，重复1,2步骤(作HI)；
4、找出1,2,3所作的两条直线的交点，这个交点就是圆心；
5、选择三角形其中一条边，作直线LM=2n，LM⊥BC交AC于点L，交BC于点M；
（注：第5步也可以改为“作直线LM=2n，LM⊥BC交AB于点L，交BC于点M”；）
6、以O为圆心，OM为半径画圆，这个圆就是所求圆。

下面是“数学研发论坛”的hujunhua版主给出的一种作法：

作法：
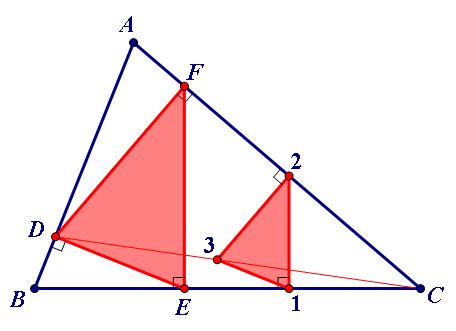
先作△ABC的一个旋转了90度的小相似形△123，它几乎内接于△ABC（两顶点落在△ABC的两边上），然后通过位似变换达到内接。具体作法如下。

1、在BC边上任取点1，作BC的垂线交AC于2，
2、过2作AC的垂线，过1作A垂线，两垂线相交于3
3、连结直线C3，交AB于D
4、过D作AB的垂线交BC于E
5、过D作到AC的垂线段DF
6、D，E，F的外接圆

转载到请包括本文地址：https://kexue.fm/archives/744

更详细的转载事宜请参考：《科学空间FAQ》