三角半分正方形

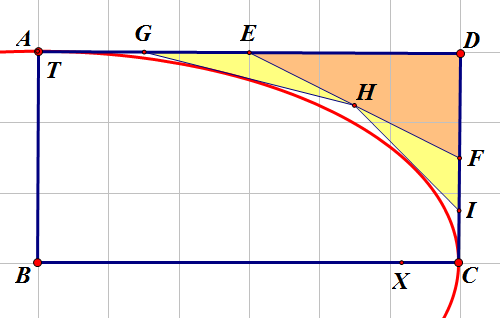
印象中我在初一曾从一个美术生好朋友那里学到了一个画椭圆的方法：选取一个矩形，取一组邻边的中点，连接并切除得到的三角形；在剩下的五边形中，继续取邻边中点，连接，切除，得到一个如下图的图形；然后作一个尽可能与下图AG、GH、HI、IJ相切的弧，这个弧就大概为四分之一的椭圆了。

我以为只要无限对半分下去，就可以得到一个精确的椭圆。但很快我就推翻了这个结论，原因很简单，考虑下边的图形（边长为1的正方形），要是我的结论正确的话，那么这个图形应该收敛于一个四分之一的圆，它的弧长应该收敛于$\frac{\pi}{2}$。但是利用勾股定理算一下就会发现切出来的多边形的侧边长（除了两条最长的直角边）之和很快就会少于$\frac{\pi}{2}$。

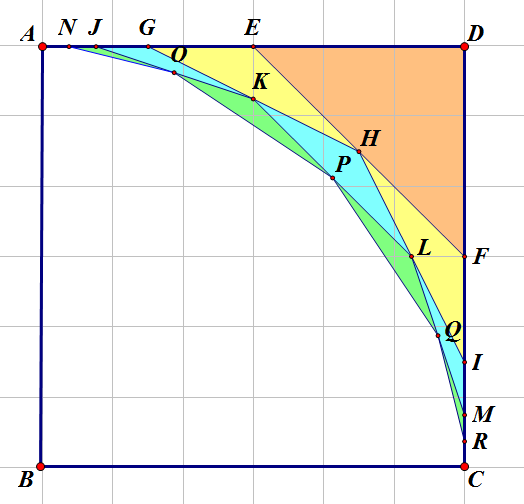
那么这个对半分的极限会是什么图形呢？我原来以为会得到一条有趣的曲线，但前几天计算让我知道，这并不是什么令人兴奋的曲线——最终的结果是——三角形ABC！对，这个切割方法居然可以把一半的正方形给切掉了。（幸好我的好朋友只进行了有限步的切割）下面我们来试着证明这个结论。

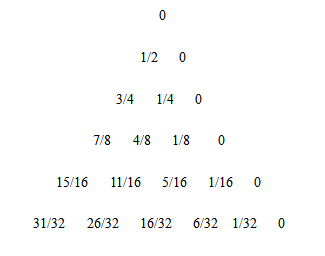
我们首先来看看这些点的分布规律。把D点当成原点，A点是(1,0)，C点是(0,1)，那么可以列出下表

这是一个类似杨辉三角的数阵，其中每个坐标是上面两个相邻坐标的平均数；而两端是$(\frac{2^n-1}{2^n},0)$的形式。为了更清晰地看出规律，我们只看x坐标：

不难看出，第(n+1)行的数字的分母都是$2^n$，而把相邻的两个分子求差，恰好是杨辉三角的第n行，即第(n+1)行的第i个数为：
$$\frac{2^n-C_n^0-C_n^1-...C_n^{i-1}}{2^n}$$

为了证明最终的曲线趋于一条直线，我们只需要证明中点坐标趋于$(1/2,1/2)$即可。为此，我们考虑第(2n+1)行的数字，其中点坐标为(k,k)，其中
$$k=\frac{2^{2n}-C_{2n}^0-C_{2n}^1-...C_{2n}^n}{2^{2n}}$$

根据$C_{2n}^0+C_{2n}^1+C_{2n}^2+...+C_{2n}^{2n}=2^{2n}$，k可以改写成
$$k=\frac{2^{2n}-\frac{2^{2n}+C_{2n}^n}{2}}{2^{2n}}=1/2-\frac{C_{2n}^n}{2^{2n+1}}$$

现在问题就在于当n趋于无穷时，$\frac{C_{2n}^n}{2^{2n+1}}$是否会趋于0。BoJone用手头上的科学计算器代入n=50计算，发现结果等于0.036...这并没有显示收敛的迹象，但计算器的极限只能算到n=50.于是没有办法，要另觅他法了。由于$C_{2n}^n=\frac{(2n)!}{(n!)^2}$，由斯特灵公式：
$$lim_{n\to \infty} \sqrt{2\pi n} (\frac{n}{e})^n //n! =1$$

于是$(n!)^2=2\pi n (\frac{n}{e})^{2n},(2n)! =2\sqrt{\pi n} (\frac{2n}{e})^{2n}$，即
$$C_{2n}^n=2^{2n}\cdot \frac{1}{sqrt{\pi n}}$$

最后得到：$lim_{n\to \infty} \frac{C_{2n}^n}{2^{2n+1}}=lim_{n\to \infty} \frac{1}{2 sqrt{\pi n}}=0$

严格来讲，上述推导过程用等号是不对的。但是由于我们只是求极限，极限是具有传递性，因此这样写也没有多大问题。至此我们证明了切割后的图形的中点趋于$(1/2,1/2)$，即最后得到的是一条直线！

转载到请包括本文地址：https://www.kexue.fm/archives/1471

更详细的转载事宜请参考：《科学空间FAQ》