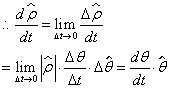
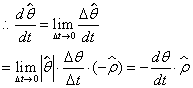
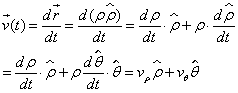
 (图四)
(图四)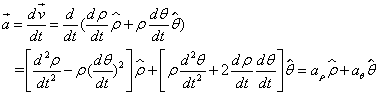
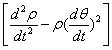
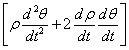
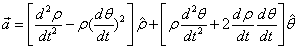
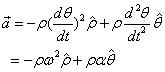
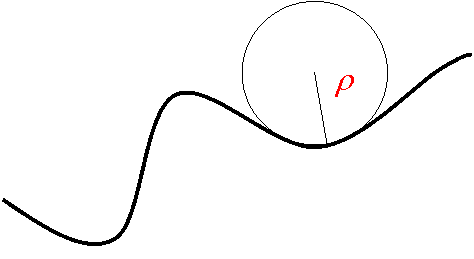
| 【上一页】【下一页】【返回目录】 | |
| §1-3 圆周运动及其描述 | |
| 1. 平面极坐标系 | |
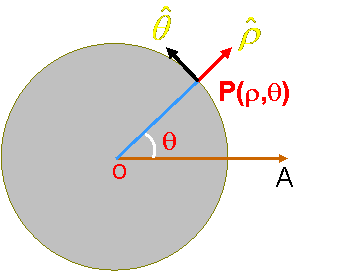
| 处理圆周运动一类的平面运动时,直角坐标系不方便。这时广泛采用的是平面极坐标系。 | |
| 如图一, |
|
| |
|
  |
|
| (图一) (图二) | |
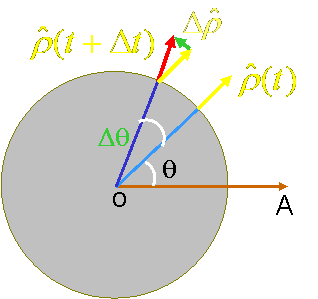
| 2. 单位矢量 | |
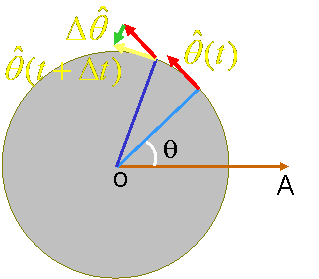
| 对于极径单位矢量: | |
| |
|
| 其大小为: | |
| |
|
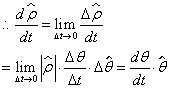 |
|
| 同样,对于极角单位矢量: | |
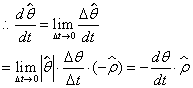 |
|
 |
|
| (图三) | |
| 3. 圆周运动 | |
| 引入极坐标系后,圆周运动的运动学方程为: | |
| |
|
| 因此,质点的速度为: | |
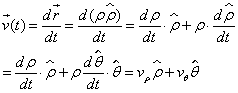 |
|
| 径向速度: |
|
| 横向速度: |
|
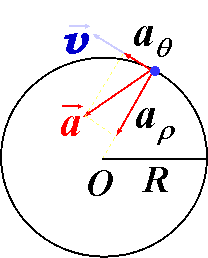
| 通常圆周运动时径向速度为0,这时: |  (图四) (图四) |
| |
|
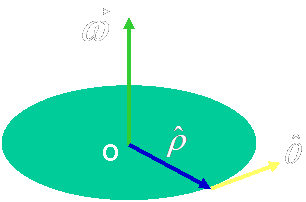
| 这时常引入角速度矢量 |
|
| 定义:大小: |
|
| 方向: |
|
| 质点的加速度为: | |
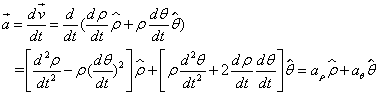 |
|
| 径向加速度: | |
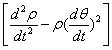 |
|
| 横向加速度: | |
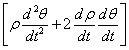 |
|
| 讨论: | |
| ⅰ° 直线运动: | |
| |
|
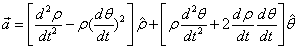 |
|
| ⅱ° 圆周运动: | |
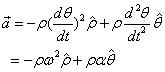 |
|
| 其中 |
|
| ⅲ° 匀速圆周运动: | |
| |
|
 |
|
| (图五) | |
| 3.平面曲线运动 | |
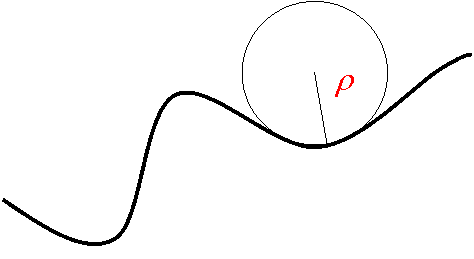 |
|
| (图六) | |
| 一个任意的平面曲线运动,可以视为由一系列小段圆周运动所组成。 | |
| §1-4 运动描述的相对性(自学) | |
| §1-5 伽利略坐标变换(自学) | |