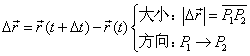
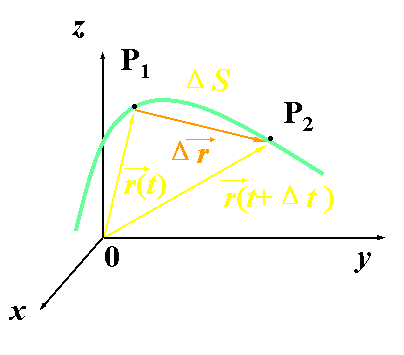
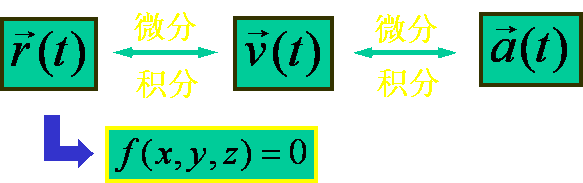
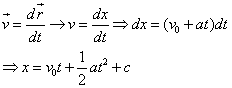
【上一页】【下一页】【返回目录】
§1-2 位移 速度 加速度
1. 位矢（position vector）
　　位置矢量（位矢、矢径）：用来确定某时刻质点位置（用矢端表示）的矢量。
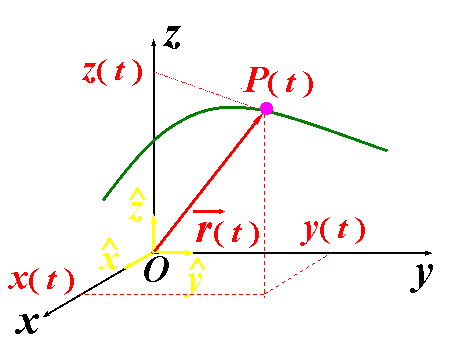
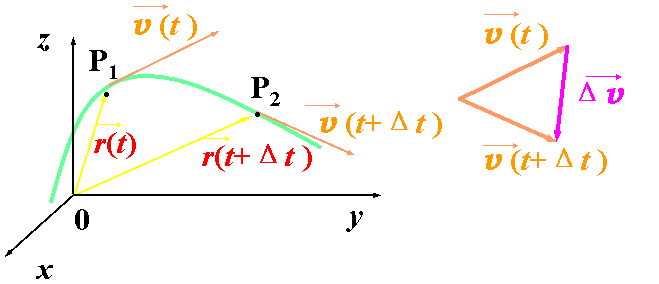
　　下面是一幅矢量图(图一) ：
　　　　　　　　　　　（图一）
P(t)点位置矢量：
　　
　 　
　　　
2. 运动函数（function of motion）
机械运动是物体（质点）位置随时间的改变。即：位矢是时间t的函数。
　　
　　　　　　—— 运动函数（运动方程 ）。
也可以写为：
或者：
　　　
　　　
消去时间t,得到轨迹方程:
下面是一个运动函数的例子：
 
3. 位移（displacement）
位移：质点在一段时间内位置的改变。
图二中：
　　
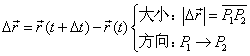路程：标量
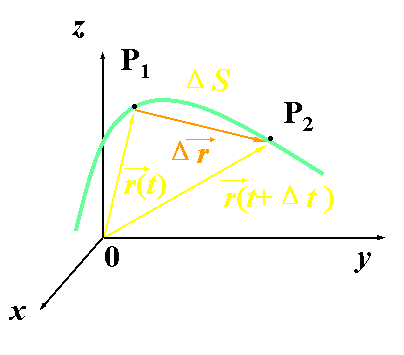　　　　　　　　　　　　　　　　（图二）
4. 速度（velocity）
质点位矢对时间的变化率叫速度。反映质点运动快慢的物理量。
ⅰ° 平均速度：
　　
　　　　——矢量
ⅱ° 平均速率：
　　
　　　　——标量
ⅲ° 瞬时速度
　　
　　　　——矢量
ⅳ° 瞬时速率
　　
　　　　——标量
平均速度与所取的时间间隔有关，时间间隔越短，平均速度就越接近于瞬时速度。瞬时速度的方向是切线方向。
速率只反映大小，没有方向。
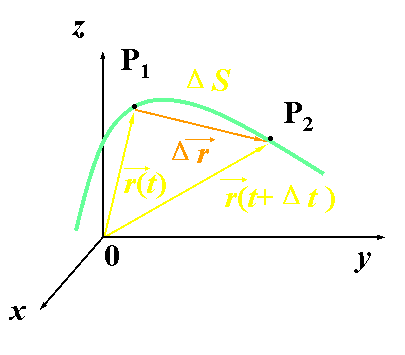　　　　　　　　　　　　　　（图三）
5. 加速度（acceleration）
质点速度对时间的变化率叫加速度。
　　　　　　　　　　　　　　　　　　（图四）
平均加速度：
　　
瞬时加速度：
　　
6. 描述质点运动的状态参量的特性
　　状态参量包括：
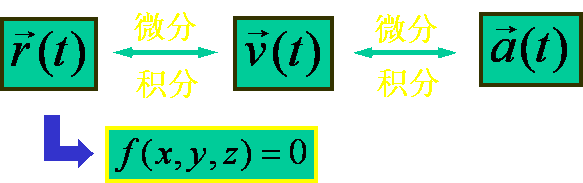（1）矢量性。注意矢量和标量的区别。
（2）瞬时性。注意瞬时量和过程量的区别
（3）相对性。对不同参照系有不同的描述。
例1：一质点在xy平面运动，其运动函数为，，其中R，为常量。
　　　求质点的运动轨迹及任一时刻的位矢、速度、加速度？
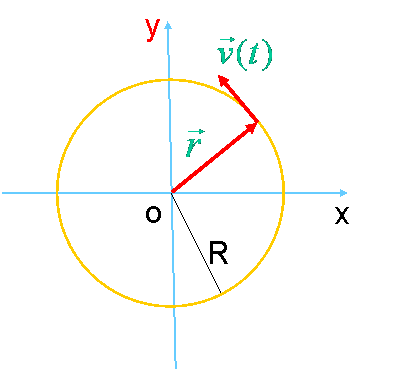
解：质点的运动轨迹如图五所示。
ⅰ° 对x，y两函数平方相加得：
　　
ⅱ° 任一时刻的位矢：
　　
ⅲ° 速度
　　
　　　　　　　　　　　　　（图五）
其分量为：
　　
速率：
　　
ⅳ° 加速度：
　　
　　　
表明加速度方向与位矢相反，指向圆心。 大小为 ．
可以看出，利用求导，很方便将位矢、速度、加速度等量联系起来。
 
例2：求匀加速直线运动的运动方程。已知质点加速度为a。
解：在一维情况下，矢量可以简化为标量。
　　
则有：
　　
设初始速度为V0，则，V = V0+at
再由定义：
　　
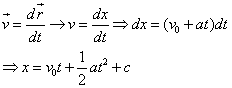由初始条件C=X0,定为原点，则：
　　
 
例3：如图六，拉船速度V0一定，高度为H。求小船向岸边移动的速度和加速度。
　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　　（图六）
解：设小船到o点的距离是L，则：
　　
对时间求导：
　　
其中 就是小船速度,而
所以有:
　　
加速度:
　　
　　
　　　　　　　　　　　　　　　　　　　
【上一页】【下一页】【返回目录】
 
"

科学空间整理"