第五章狭义相对论 §5.2 狭义相对论时空观

§5.2 狭义相对论时空观( Space-Time of Special Relativity )

　　1、基本假设

　　　　爱因斯坦首先放弃了以太论观点，提出了狭义相对论的基本原理。

　　　　ⅰ°狭义相对论的相对性原理（Einstein’s principle of relativity ）：

　　　　　　所有惯性参照系都是等价的。物理定律在所有惯性系中的表达形式都相同。

　　　　ⅱ°光速不变原理（principle of constant speed of light）：

　　　　　　在所有惯性系中，真空中的光速具有相同的量值C。

　　2、相对论的时空观

　　　　在相对论中，一个突出的新概念就是“同时的相对性”。爱因斯坦建立狭义相对论就是首先从这里突破的。

　　　　ⅰ°“同时”的相对性

　　　　动画3－7表示了同时相对性原理：

　　　　结论：

　　　　　　沿两惯性系S和S’相对运动方向发生的两个事件，若S中是同时发生的，则S’中就不是同时发生的了。这就是同时性的相

对性原理。

　　　　ⅱ°时钟推迟

　　　　讨论一个匀速运动的钟和一系列“静止”的同步的钟的比较。（见动画3－8）

　　　　对于小张：

　　　　　　　　　　　　　　　　　　　　　　　　（１）

　　　　对于小王：

　　　　由于光速不变：

　　　　　　　　　　　　　（２）

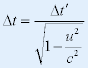
　　　　由(1)、(2)解得：

—— 原时（proper time）：同一地点两事件的时间间隔。由上式，原时最短。

　　　　一个运动的钟C’和一系列静止的钟C1、C2…比较，运动的钟变慢了。一个运动的钟的“一秒”比一系列静止的钟的“一

秒”要长，这就是所谓的“时间膨胀（推迟）”。

　　　　时间膨胀完全是一种相对效应。

　　　　1971年，美国空军用两组CS（铯）原子钟绕地球一周，得到运动钟变慢：203±10ns，而理论值为：184±23ns，在误差

范围内二者相符。

　　　　应该注意，与钟一起运动的观测者是感受不到钟变慢的效应的。

　　ⅲ°长度缩短

　　　　具体的长度缩短效应见动画3－9。

　　　　运动尺长度的测量：

　　　　　　事件1： B与计时器对齐；事件2： A与计时器对齐。

　　　　车下看（原时）：

　　　　动长：

　　　　车上看：

　　　　静长(原长)：

　　　　∴ 原长最长

　　　　总结（请点击动画3-1-32）：

(动画3-1-32)