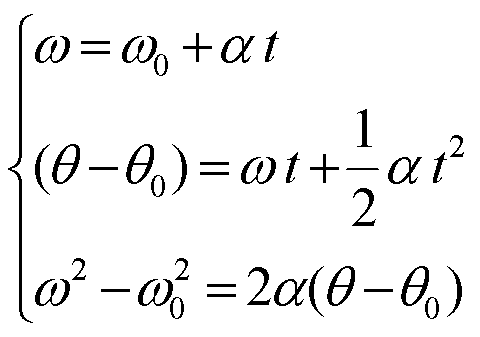v质点的运动只代表物体的平动，物体是有形状、大小的，它可以平动、转动，甚至更复杂的运动。因此，对于机械运动的研究，

只限于质点的情况是不够的。

v刚体是一种特殊的质点系统，无论在多大外力作用下，系统内任意两质点间的距离始终保持不变。刚体即运动过程中没有形变的

物体。

v刚体考虑了物体的形状和大小，但不考虑形变，刚体同质点一样，也是一个理想模型。

刚体在运动过程中，体内任一给定直线（或任意二质点间的连线）在空间的指向始终保持平行。

描述刚体的平动，可以用一点的运动来代表，通常选择质心来代表整个刚体的运动。

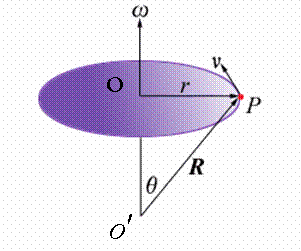
如果刚体上所有的质点都绕同一直线作圆周运动，这种运动称刚体的转动，这条直线称转轴。

若转轴是固定的，就叫定轴转动（rotation about a fixed axis）。

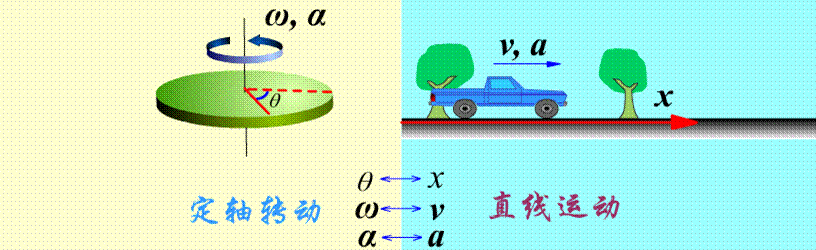
刚体的一般运动 = 平动 + 转动

ⅰ  刚体定轴转动时，刚体上各点都绕同一直线（转轴）作圆周运动，而轴本身在空间的位置不变。

ⅱ 过刚体上任意一点并垂直于转轴的平面称为转动平面。显然，转动平面可以做无限多个，它们是等价的。刚体上所有的点都绕转

角速度ω

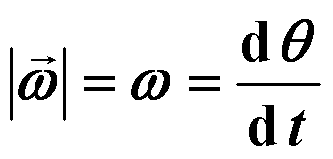
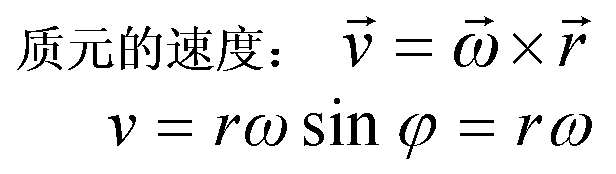
从角速度与角加速度的这种关系出发, 我们可以把质点沿直线运动的位移、速