－－称力臂
称冲量矩——力矩对时间的积累作用。
的条件可知，它可以是
；也可以是
；还可以是
与
的夹角之正弦为零。始终沿(
)方向，因此有：
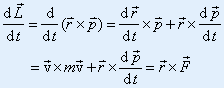
| §3.6 质点的角动量和角动量守恒定律 |
| （angular momentum of a particle and the law of conservation of angular momentum） |
| 1. 质点的角动量 |
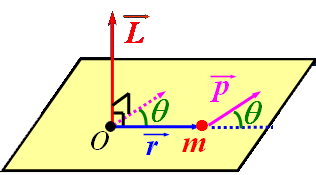
| 角动量是质点运动的另一个重要物理量。质点m对固定点 O的角动量定义为： |
| |
| 由叉乘的定义，角动量大小： |
| |
| 单位： kg·m2/s 或 J·s |
| 角动量的方向由右手定则决定。 |
| |
| （图一） |
| 角动量与位矢有关，因此，说明角动量时，必须指明相对的ｏ点。 |
| 2. 力矩 (Torque) |
| 由牛顿第二定律可知，质点的动量的变化率是由质点受的合外力决定的。那么质点的角动量变化率又由什么决定呢？ |
| |
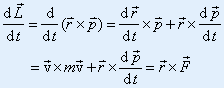| 定义力对定点 O 的力矩为： |
| |
| 力矩的大小 |
| －－称力臂 |
| 力矩的单位（SI）是 N·m |
| 力矩的方向由右手定则决定 |
| 于是有 |
| |
| 或 |
| 质点所受的合外力矩等于它的角动量对时间的变化率。这就是质点的角动量定理。 （微分形式） |
| 积分： |
| |
| 质点角动量定理（积分形式） |
| 称冲量矩——力矩对时间的积累作用。 |
| 3. 角动量守恒定律 |
| 在质点的角动量定理中，特殊地： |
| |
| 就是说，如果对某一固定点，质点所受的合外力矩为零，则此质点对该固定点的角动量矢量保持不变。 |
| ——质点角动量守恒定律 |
| ⅰ°角动量守恒定律是物理学的基本定律之一，它不仅适用于宏观体系，也适用于微观体系，而且在高速低速范围均适用。 |
| ⅱ°由的条件可知，它可以是；也可以是；还可以是与的夹角之正弦为零。 |
| 例：证明行星运动的开普勒第二定律。即：行星对太阳的矢径在相同的时间扫过相同的面积。 |
| 证明： |
| 行星受的引力始终沿()方向，因此有： |
| |
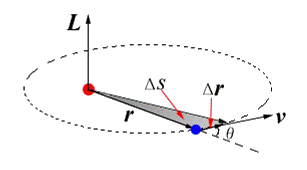
| 即：行星运动过程中，相对于太阳的角动量不变。由图一： |
| |
| （图一） |
| |
| |
| |
| |
| 总结: |
|