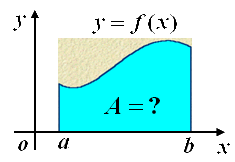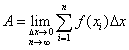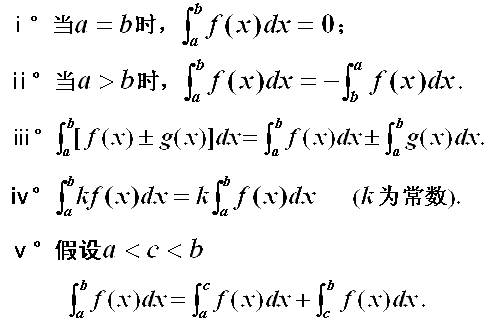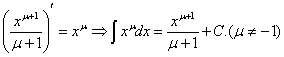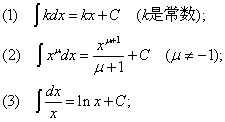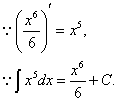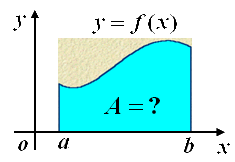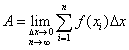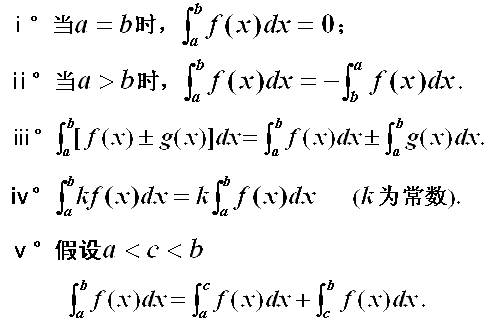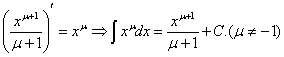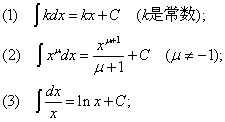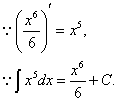| 【上一页】【下一页】【返回目录】 |
| 6. 积分 |
| 1)问题的提出——求曲边梯形的面积 |
| 可以用矩形面积近似取代曲边梯形面积. 显然,小矩形越多,矩形总面积越接近曲边梯形面积. |
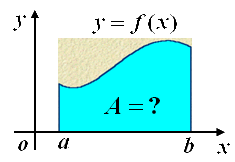 |
| (图一) |
| 图二中用四个小矩形逼近 |
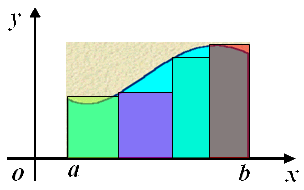 |
| (图二) |
| 图三中用九个小矩形逼近 |
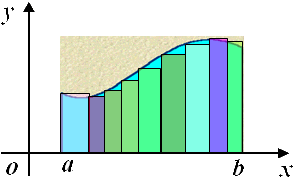 |
| (图三) |
| 曲边梯形面积的近似值为: |
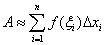 |
| 当等分间隔无穷多时: |
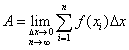 |
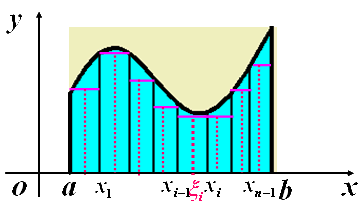 |
| (图四) |
| 2)定积分的定义 |
上式的这个极限称为函数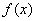 在区间 在区间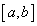 上的定积分,记为: 上的定积分,记为: |
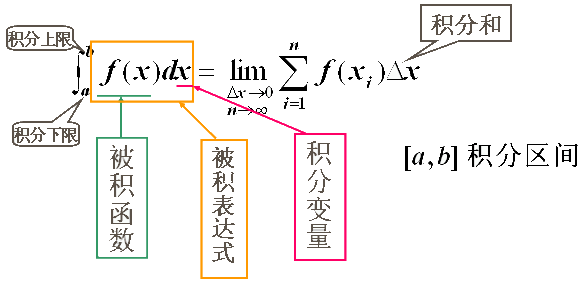 |
| 3)定积分的几何意义 |
| 曲边梯形的面积: |
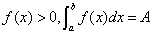 |
| 曲边梯形的面积的负值: |
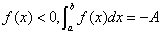 |
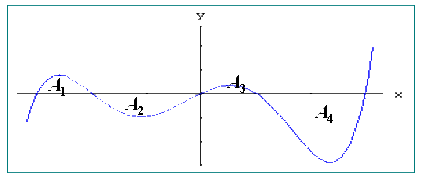 |
| (图五) |
| 图五中曲线与坐标轴所围区域的面积为: |
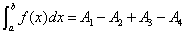 |
| 4)定积分的性质 |
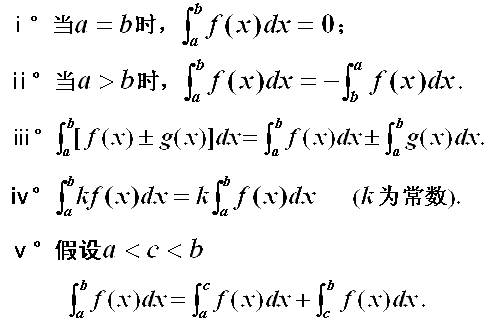 |
| 5)原函数与不定积分的概念 |
| 定义: |
如果在区间 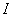 内,可导函数 内,可导函数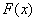 的导函数为 的导函数为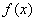 ,即 ,即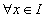 ,都有 ,都有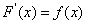 或 或 |
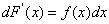 ,那么函数 ,那么函数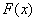 就称为 就称为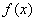 或 或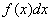 在区间 在区间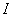 内的原函数。 内的原函数。 |
| |
| 例: |
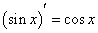 , ,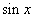 是 是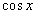 的原函数. 的原函数. |
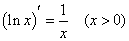 , ,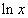 是 是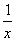 在区间 在区间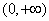 内的原函数. 内的原函数. |
| 原函数并非唯一,如: |
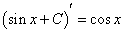 ,C为任意常数 ,C为任意常数 |
| |
| 不定积分的定义: |
在区间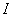 内,函数 内,函数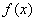 的带有任意常数项的原函数称为 的带有任意常数项的原函数称为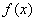 在区间 在区间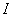 内的不定积分, 内的不定积分, |
记为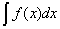 . . |
 |
| 6)积分的基本计算 |
| ⅰ°由不定积分的定义可知,寻找原函数是计算的关键 |
| 例如: |
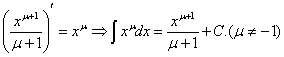 |
| 微分运算与求不定积分的运算是互逆的,因此可以根据求导公式得出积分公式. 如: |
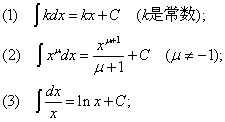 |
| ⅱ°定积分是特殊条件下的不定积分 |
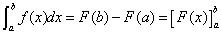 |
| 这称为牛顿—莱布尼茨公式 |
| 例1:求 |
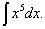 |
| 解: |
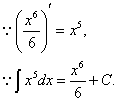 |
| 例2: 求 |
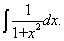 |
| 解: |
 |
| 例3:求 |
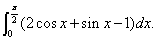 |
|
解: |
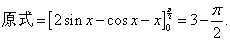 |
| |
| 结束语: |
| 发展独立思考和独立创新的一般能力,应当始终放在首位,而不应当把知识放在首位。如果一个人掌握了他 |
| 的学科的基础理论,并且学会了独立思考与工作,他必定会找到自己的道路。而且比起那些主要以获取细节知识为其 |
| 训练内容的人来,他一定会更好适应进步和变化. |
| --爱因斯坦 |
|
| |