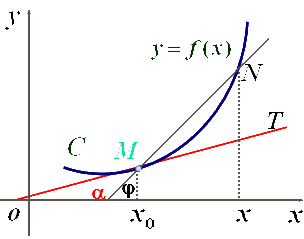 (图一)
(图一)
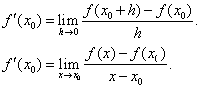
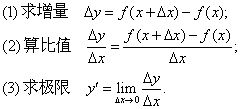
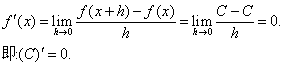
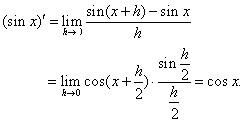
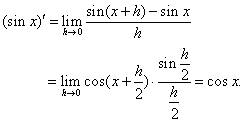
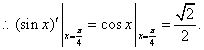

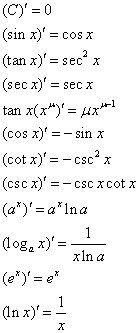
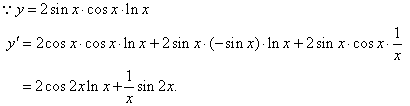
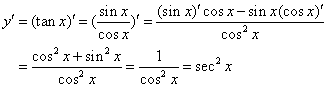
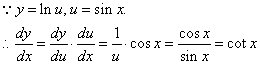
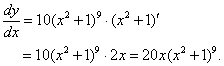
| 【上一页】【下一页】【返回目录】 |
| 4. 导数 |
| 1)问题的提出——切线问题 |
| 如图一,如果割线MN绕点M旋转而趋向极限位置MT,直线MT就称为曲线C在点M处的切线. |
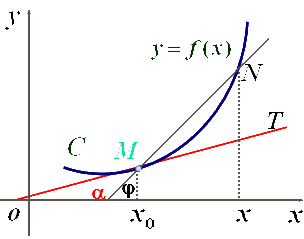 (图一) (图一) |
| 极限位置即: |
| |
| |
| |
| |
| 2)导数的定义 |
| 定义: |
 |
| 即: |
| |
| 其它形式: |
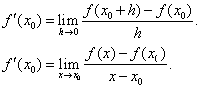 |
| 应当指出,函数 f(x) 的导数 f'(x) 本身也是x的一个函数,因此我们可以再取它对x的导数,这叫函数 y = f(x) 的二阶导数。 |
| |
| 依此类推,可以定义高阶导数。 |
| 3)导数的几何意义 |
| 切线方程为: |
| 4)由定义求导数 |
| 步骤: |
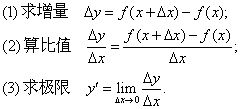 |
| 例1: |
| 解: |
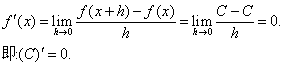 |
| 例2: |
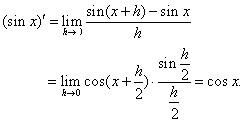 |
| 解: |
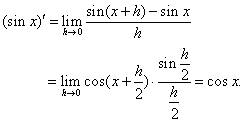 |
| 即 |
| |
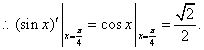 |
| 5)导数的运算 |
| ⅰ°和、差、积、商的求导法则 |
 |
| ⅱ°基本初等函数的导数公式 |
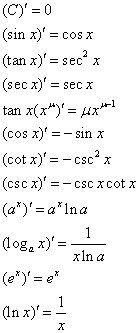 |
| ⅲ°复合函数的求导法则 |
| |
| 利用上述公式及法则初等函数求导问题可完全解决. |
| 例1: |
| |
| 解: |
| |
| 例2: |
| |
| 解: |
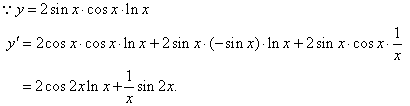 |
| 例3: |
| |
| 解: |
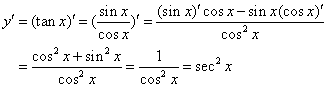 |
| 例4: |
| |
| 解: |
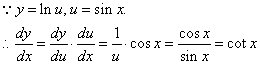 |
| 例5: |
| |
| 解: |
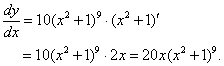 |